$2$ 次と $3$ 次の行列式
2022-09-22
大学の授業や教科書では置換について学んだ直後に天下り式に行列式の定義を学ぶことが多いようです。
完成した数学を学ぶという立場にたてば、天下り式に導入してしまった方が回り道をせずに効率良く学べるということなのでしょう。 しかし、天下り式にいきなり定義される行列式は、意味を読み取ることが困難な形をしているため、「これって一体何なの?」という感想を持つことが多いかもしれません。(これではちょっと迷惑な?天からの?贈り物になってしまうかもしれませんね。)
行列式は、歴史的には連立一次方程式の解法を研究する過程で、行列の概念より先に発見されたようです。しかし、歴史の順に学んで行くのもかなりの回り道になるでしょう。
そこで、ここでは妥協案として、まず、2次の場合について、「逆行列の存在を判定するための道具としての行列式」を定義することにします。次に、このような観点から定義された 2次の行列式に対して代数的な性質や幾何ベクトルの世界との関係を明らかにします。そしてさらに、明らかにされた2次の行列式の性質や関係を利用して、3次の場合の行列式を定義してみることにします。
回り道をせずに行列式の一般論を早く知りたい人は、このページをとばして先へ進んでも良いでしょう。
\(2\) 次の行列式
逆行列の存在を判定する道具としての行列式
\(2\) 次の正方行列 \(A=\left(\begin{array}{c}a & b\\c & d\end{array}\right)\) がどんな行列ならば逆行列をもつのか考えてみることにします。
もし、\(A\) に逆行列 \(X=\left(\begin{array}{c} x & y\\ z & w\end{array}\right)\) が存在するならば、\[ \left(\begin{array}{c} a & b\\ c & d\end{array}\right) \left(\begin{array}{c} x & y\\ z & w\end{array}\right) = \left(\begin{array}{c} 1 & 0\\ 0 & 1\end{array}\right) \]
\[ \begin{align} ax+bz&=1 \tag{1}\\ ay+bw&=0 \tag{2}\\ cx+dz&=0 \tag{3}\\ cy+dw&=1 \tag{4} \end{align} \]
が成り立ちます。
行列 \(A\) に逆行列があるのかどうか知りたければ、\(a,b,c,d\) を与えられている数として考え、\(x,y,z,w\) が求められるかどうか考えてみればよいわけです。
まず、\((1)\) 式、\((3)\) 式を組合せて \(x\) と \(z\) を求める方針で計算を進めることにします。
\(z\) を消去して \(x\) だけの式を得るために \((1)\times d -(3) \times b\) をやってみると
\[\begin{align} adx+bdz&=d \\ -)\quad bcx+bdz&=0\\ \hline (ad-bc)x &= d \end{align}\] となります。同様に、\(x\) を消去して \(z\) だけの式を彫るために、\((1)\times c -(3) \times a\) をやってみると \[(ad-bc)z= a\] が得られます。
つまり、\((1)\) 式、\((3)\) 式を組合せると、\[\begin{align} (ad-bc)x &= d \tag{5}\\ (ad-bc)z &= a \tag{6} \end{align}\]
が得られるわけです。
同様にして\((2)\) 式、\((4)\) 式を組合せると、\[\begin{align} (ad-bc)y &= -b \tag{7}\\ (ad-bc)w &= -c \tag{8} \end{align}\]
が得られることがわかります。
\(ad-bc=0\) の場合、\((5)\),\((6)\),\((7)\),\((8)\) より \(a=b=c=d=0\) ということになりますが、このとき \(A\) は零行列になっています。零行列には逆行列があるはずはありませんからこれは却下です。
\(ad-bc \neq 0\) の場合、\((5)\),\((6)\),\((7)\),\((8)\) より、
\[\begin{align} x&= \frac{d}{ad-bc}\\ y&= \frac{-b}{ad-bc}\\ z&= \frac{-c}{ad-bc}\\ w&= \frac{a}{ad-bc}\\ \end{align} \] となります。
以上をまとめると次のようになります。
\(2\) 次の正方行列 \(A=\left(\begin{array}{c} a & b\\ c & d\end{array}\right)\) に逆行列があるのは \(ad-bc \neq 0\) のときで、そのとき逆行列 \(A^{-1}\) は\[A^{-1} = \frac{1}{ad-bc}\left(\begin{array}{c} d & -b\\ -c & a\end{array}\right)\]
で与えられます。
この事実により、\(ad-bc\) は逆行列の存在を判定できる重要な数であることがわかりました。そこでこれに名前をつけ、記号を用意することにします。
定義
\(2\) 次の正方行列 \(A=\left(\begin{array}{c} a & b\\ c & d\end{array}\right)\) に対して、\(ad-bc\) を計算して得られる数を \(A\) の行列式といい、 \(\det(A)\) という記号であらわします。
補足:正確には、上で定義されたものは行列式の値と呼ばれます。つまり、さまざまな行列 \(A=\left(\begin{array}{c} a & b\\ c & d\end{array}\right)\) に対して、\(ad-bc\) を計算して得られる数を対応させる関数を行列式と言い、上の定義では言葉を乱用して関数の値を行列式と呼んでいます。
\(2\) 次の正方行列の積と \(2\) 次の行列式
命題
2つの \(2\) 次の正方行列 \(A,B\) に対して \[\det(AB)=\det(A)\det(B)\] が成り立ちます。
証明
これは\[ A=\left(\begin{array}{cc} a & b \\ c & d \end{array}\right)\,,\, B=\left(\begin{array}{cc} e & f \\ g & h \end{array}\right) \]
とおいて、\(\det(AB)\) と \(\det(A)\det(B)\) を行列式の定義に従って計算してみれば確認できます。ぜひ一度、自分の手を動かして計算してみてください。
\(2\) 次の行列式の性質
行列を列ごとに区分けしてできるベクトルと行列式の関係を調べてみようと思います。
そこで次のように、行列 \(A =\left(\begin{array}{c} a & b\\ c & d\end{array}\right)\) を
\[ A =\left(\boldsymbol{a} \,\,\, \boldsymbol{b}\right),\, \text{ここで}\,\, \boldsymbol{a}=\left(\begin{array}{c}a\\c \end{array}\right),\,\boldsymbol{b}=\left(\begin{array}{c}b\\d \end{array}\right)\]
のように列ベクトルに区分けして考え \(A\) の行列式 \(\det(A)\) を \(\det(\boldsymbol{a},\boldsymbol{b})\) と書くことにします。そして \(A\) の行列式 は2つの列ベクトル \(\boldsymbol{a}\) と \(\boldsymbol{b}\) で決まる数と思うことにしましょう。
実は \(\det(\boldsymbol{a},\boldsymbol{b})\) は以下のような性質を持っています。
2重線形性
命題
列ベクトル \(\boldsymbol{a},\boldsymbol{b},\cdots\) などと数 \(r\) について \[\begin{align} \det(\boldsymbol{a_1}+\boldsymbol{a_2},\boldsymbol{b}) &=\det( \boldsymbol{a_1} ,\boldsymbol{b})+\det(\boldsymbol{a_2},\ \boldsymbol{b} )\\ \det(\boldsymbol{a},\boldsymbol{b_1} +\boldsymbol{b_2}) &=\det( \boldsymbol{a},\boldsymbol{b_1}) +\det(\boldsymbol{a},\ \boldsymbol{b_2} )\\ \det(r\boldsymbol{a},\boldsymbol{b}) &=r\det( \boldsymbol{a} ,\boldsymbol{b})\\ \det(\boldsymbol{a},r\boldsymbol{b}) &=r\det( \boldsymbol{a} ,\boldsymbol{b})\\ \end{align}\] が成り立ちます。
これは、言葉でいうと
- \(\det(\boldsymbol{a}, \boldsymbol{b})\) は1番目の変数(変ベクトルというべき?) \(\boldsymbol{a}\) について和を保つ
- \(\det(\boldsymbol{a}, \boldsymbol{b})\) は2番目の変数(変ベクトルというべき?) \(\boldsymbol{b}\) について和を保つ
- \(\det(\boldsymbol{a}, \boldsymbol{b})\) は1番目の変数(変ベクトルというべき?) \(\boldsymbol{a}\) についてスカラー倍を保つ
- \(\det(\boldsymbol{a}, \boldsymbol{b})\) は2番目の変数(変ベクトルというべき?) \(\boldsymbol{b}\) についてスカラー倍を保つ
ということです。
交代性
命題
列ベクトル \(\boldsymbol{a},\boldsymbol{b}\) について \[\det(\boldsymbol{a},\boldsymbol{b}) =-\det( \boldsymbol{b},\boldsymbol{a}) \\\] が成り立ちます。 そしてこのことから \[\det(\boldsymbol{a},\boldsymbol{a}) = 0\] となることを導くことができます。 なぜなら、\(\det(\boldsymbol{a},\boldsymbol{a}) =-\det( \boldsymbol{a},\boldsymbol{a})\) となるので、こうなるのは \(\det(\boldsymbol{a},\boldsymbol{a}) = 0\) のときだからです。
これは、言葉でいうと
- \(\det(\boldsymbol{a},\boldsymbol{b})\) は1番目と2番目の変数(変ベクトルというべき?)を入れ替えると値はマイナス1倍になる
- \(\det(\boldsymbol{a},\boldsymbol{b})\) は1番目と2番目の変数(変ベクトルというべき?)が同じならば値は \(0\)
ということです。
以上紹介した2重線形性と交代性は、計算により簡単に確かめることができます。たとえば、2重線形性の2つ目の式は、\[\boldsymbol{a}= \left(\begin{array}{c}a\\ c\end{array}\right), \boldsymbol{b_1}= \left(\begin{array}{c}b_1\\ d_1\end{array}\right), \boldsymbol{b_2}=\left(\begin{array}{c}b_2\\ d_2\end{array}\right)\]
\[\begin{align}\det(\boldsymbol{a},\boldsymbol{b_1} +\boldsymbol{b_2})&=a(d_1+d_2)-(b_1+b_2)c \\[6pt] &= ad_1+ad_2-b_1c-b_2c\\[6pt] &=(ad_1-b_1c)+(ad_2-b_2c)\\[6pt] &=\det( \boldsymbol{a},\boldsymbol{b_1}) +\det(\boldsymbol{a},\ \boldsymbol{b_2}) \end{align}\]
のようにして確かめることができます。
平面幾何ベクトルで \(2\) 次の行列式を図形的に考えてみると
実は、これから説明するように、平面に右手系の直交座標系を設定して座標を使って平行四辺形の面積を計算すると行列式が出現することがわかります。
\(\boldsymbol{a},\boldsymbol{b}\) は \(2\) 次の幾何ベクトルとします。つまり、どちらも平面のベクトルで矢印であらわされるものとします。
また、これらのベクトルは、平面に右手系の正規直交座標系を設けることにより成分で、\[ \boldsymbol{a}=\left(\begin{array}{c}a\\c\end{array}\right),\,\boldsymbol{b}=\left(\begin{array}{c}b\\d\end{array}\right)\]
とあらわされているとします。
ここで次のような、 \(\boldsymbol{a},\boldsymbol{b}\) で“張られる”平行四辺形の面積について考えることにします。
ここでは \(\boldsymbol{a}\) を底辺と考え、高さを求めることにしますが、そのために \(\boldsymbol{a}\) に垂直な幾何ベクトル \(\boldsymbol{u}\) を考えてみます。次の図を見てください。
とりあえずそのようなものとして \[\boldsymbol{u}=\left(\begin{array}{r}-c\\a\end{array}\right)\] または \[\boldsymbol{u}=\left(\begin{array}{r}c\\-a\end{array}\right)\] を採用することができます。
実際、どちらの場合でも \(\boldsymbol{a}\) と \(\boldsymbol{u}\) の内積を計算してみると \(0\) になることはすぐにわかりますから、これらは \(\boldsymbol{a}\) に垂直です。
前者は、\(\boldsymbol{a}\) を「反時計回り」に \(\frac{\pi}{2}\,\mathrm{rad}\) (つまり \(90 ^\circ\))回転することで得られるもので、後者は \(\boldsymbol{a}\) を「時計回り」に \(\frac{\pi}{2}\,\mathrm{rad}\) (つまり \(90 ^\circ\))回転することで得られるものです。そしてこれら2つの \(\boldsymbol{u}\) は正反対の向きになっています。
話を進める前に、ここで、平行四辺形の辺になっている \(\boldsymbol{a}\) と \(\boldsymbol{b}\) の位置関係を2つにわけて考えておきます。
\(\boldsymbol{a}\) を「反時計回り」に \(0\,\mathrm{rad}\) から \(\pi\,\mathrm{rad}\) の範囲で回転すると \(\boldsymbol{b}\) の方向になるとき
\(\boldsymbol{a}\) を「時計回り」に \(0\,\mathrm{rad}\) から \(\pi\,\mathrm{rad}\) の範囲で回転すると \(\boldsymbol{b}\) の方向になるとき
ではそれぞれの場合に、平行四辺形の面積がどのようにあらわせるのか考えてみることにしましょう。
1.の場合
\(\boldsymbol{u}=\left(\begin{array}{r}-c\\a\end{array}\right)\) を使って議論をします。
平行四辺形の高さを計算する際、\(\boldsymbol{a}\) に垂直な幾何ベクトルの長さは \(1\) になっているものがあると良いので、 \[\boldsymbol{n} = \frac{\boldsymbol{u}}{\|\boldsymbol{u}\|}\] とおいて、\(\boldsymbol{n}\) も使うことにします。
\(\boldsymbol{b}\) と \(\boldsymbol{n}\) のなす角を \(\theta\) とおくと、
\[\begin{align} \mathrm{平行四辺形の高さ} &= \|\boldsymbol{n}\|\|\boldsymbol{b}\|\cos\theta\\ &=\boldsymbol{n}\cdot\boldsymbol{b}\\ &=\frac{\boldsymbol{u}\cdot\boldsymbol{b}}{\|\boldsymbol{u}\|}\\ &=\frac{ad-bc}{\sqrt{a^2+c^2}} \end{align}\] とあらわされます。
これより
\[\begin{align} \mathrm{平行四辺形の面積} &= \|\boldsymbol{a}\| \times \mathrm{平行四辺形の高さ} \\ &=\sqrt{a^2+c^2} \times \frac{ad-bc}{\sqrt{a^2+c^2}}\\ &=ad-bc\\ &=\det(\boldsymbol{a},\boldsymbol{b})\\ \end{align}\] となることがわかります。
2.の場合
\(\boldsymbol{u}=\left(\begin{array}{r}c\\-a\end{array}\right)\) を使って議論をします。 1.の場合と異なるのは \(\boldsymbol{u}\) の符号、\(\boldsymbol{n}\) の符号なので、 1.のときと同様に計算していくと、 \[\begin{align} \mathrm{平行四辺形の面積} &= \|\boldsymbol{a}\| \times \mathrm{平行四辺形の高さ} \\ &=\sqrt{a^2+c^2} \times \frac{-(ad-bc)}{\sqrt{a^2+c^2}}\\ &=-(ad-bc)\\ &=-\det(\boldsymbol{a},\boldsymbol{b})\\ \end{align}\] となることがわかります。
以上より、
\(\boldsymbol{a}\) を「反時計回り」に \(0\,\mathrm{rad}\) から \(\pi\,\mathrm{rad}\) の範囲で回転すると \(\boldsymbol{b}\) の方向になるときには
\[\det(\boldsymbol{a},\boldsymbol{b}) = \boldsymbol{a}\,\mathrm{と}\,\boldsymbol{b}\,\mathrm{で張られる平行四辺形の面積}\] とあらわすことができ、
\(\boldsymbol{a}\) を「時計回り」に \(0\,\mathrm{rad}\) から \(\pi\,\mathrm{rad}\) の範囲で回転すると \(\boldsymbol{b}\) の方向になるときには\[\det(\boldsymbol{a},\boldsymbol{b}) = -1\times\left(\boldsymbol{a}\,\mathrm{と}\,\boldsymbol{b}\,\mathrm{で張られる平行四辺形の面積}\right)\]
とあらわすことができることがわかりました。
つまり、\(2\) 次の行列式 \(\det(\boldsymbol{a},\boldsymbol{b})\) は 2つの平面ベクトル $$ と \(\boldsymbol{b}\) で張られる平行四辺形の面積を符号付きで考えたものに等しくなっていたわけです。
\(2\) 次の正方行列で定まる一次変換と \(2\) 次の行列式の図形的意味
\(2\) 次の正方行列 \(A=\left(\begin{array}{c} a & b\\ c & d\end{array}\right)\) は平面のベクトルの空間 \(V^2\) の一次変換を定めることができるのでした。それは、\(V^2\) の幾何ベクトル \(\boldsymbol{x}\) を \(V^2\) の幾何ベクトル \(A\boldsymbol{x}\) に対応させる写像です。この一次変換を平行四辺形の面積と関連付けてみようと思います。
\(\boldsymbol{x},\boldsymbol{y}\) を \(V^2\) の2つの幾何ベクトルとし、それらで張られる平行四辺形の面積を \(S\) とします。また、変換後の2つの幾何ベクトル \(A\boldsymbol{x},A\boldsymbol{y}\) で張られる平行四辺形の面積を \(S'\)とします。
これからこの2つの面積の値を比べることにしますが、計算の見通しを良くするために 2つの行ベクトル \(\boldsymbol{x},\boldsymbol{y}\) を横に並べた正方行列 \(X\)、つまり、 \[X=(\boldsymbol{x},\boldsymbol{y})\] を準備しておきます。すると、 \[AX=(A\boldsymbol{x},A\boldsymbol{y})\] とあらわすことができます。
話を進める前に、ここで、変換前の平行四辺形の辺になっている \(\boldsymbol{x}\) と \(\boldsymbol{y}\) の位置関係を2つにわけ、変換後の平行四辺形の辺になっている \(A\boldsymbol{x}\) と \(A\boldsymbol{y}\) の位置関係も2つにわけ、それらを組合せて全部で4通りに場合分けをすることにします。
\(\boldsymbol{x}\) を「反時計回り」に \(0\,\mathrm{rad}\) から \(\pi\,\mathrm{rad}\) の範囲で回転すると \(\boldsymbol{y}\) の方向になり、 \(A\boldsymbol{x}\) を「反時計回り」に \(0\,\mathrm{rad}\) から \(\pi\,\mathrm{rad}\) の範囲で回転すると \(A\boldsymbol{y}\) の方向になるとき
\(\boldsymbol{x}\) を「時計回り」に \(0\,\mathrm{rad}\) から \(\pi\,\mathrm{rad}\) の範囲で回転すると \(\boldsymbol{y}\) の方向になり、 \(A\boldsymbol{x}\) を「時計回り」に \(0\,\mathrm{rad}\) から \(\pi\,\mathrm{rad}\) の範囲で回転すると \(A\boldsymbol{y}\) の方向になるとき
\(\boldsymbol{x}\) を「反時計回り」に \(0\,\mathrm{rad}\) から \(\pi\,\mathrm{rad}\) の範囲で回転すると \(\boldsymbol{y}\) の方向になり、 \(A\boldsymbol{x}\) を「時計回り」に \(0\,\mathrm{rad}\) から \(\pi\,\mathrm{rad}\) の範囲で回転すると \(A\boldsymbol{y}\) の方向になるとき
\(\boldsymbol{x}\) を「時計回り」に\(0\,\mathrm{rad}\) から \(\pi\,\mathrm{rad}\) の範囲で回転すると \(\boldsymbol{y}\) の方向になり、 \(A\boldsymbol{x}\) を「反時計回り」に\(0\,\mathrm{rad}\) から \(\pi\,\mathrm{rad}\) の範囲で回転すると \(A\boldsymbol{y}\) の方向になるとき
図を頭の中に思い浮かべてみると、1.と2.は平行四辺形を裏返さない変換で、3.と4.は平行四辺形を裏返す変換ということがわかるでしょう。
では、変換前の面積 \(S\) と変換後の面積 \(S'\) を比べてみることにしましょう。
1.と 2.の場合\[ S' =\pm \det(A\boldsymbol{x},A\boldsymbol{y}) =\pm\det(AX) =\pm \det(A)\det(X)=\det(A)\cdot\{\pm\det(\boldsymbol{x},\boldsymbol{y})\}=\det(A)S \]
となることがわかります。(複合同順;複号は、上が 1.の場合で下が 2.の場合)
3.と 4.の場合\[ S' =\pm \det(A\boldsymbol{x},A\boldsymbol{y}) =\pm\det(AX) =\pm \det(A)\det(X)=-\det(A)\{\mp\det(\boldsymbol{x},\boldsymbol{y})\}=-\det(A)S \]
となることがわかります。(複合同順;複号は、上が 3.の場合で下が 4.の場合)
以上より、 \(A\) が平行四辺形を裏返さない変換のとき、変換後の平行四辺形の面積はもとの \(\det(A)\)倍になり、\(A\) が平行四辺形を裏返す変換のとき、変換後の平行四辺形の面積はもとの \(-\det(A)\)倍になるということがわかりました。
\(3\) 次の行列式
\(3\) 次の行列式を発見するための2つのアプローチ
\(3\) 次の正方行列から何かしらの方法で作られる数で、\(2\) 次のときと同様に、逆行列をもつための条件となっているものがあれば、それを \(3\) 次の行列式と呼ぶことにするという考えは自然なものです。しかし、2次の行列のときにおこなったような方法でそのようなものを見つけるとしたら、大変な計算をすることが予想されます。
そこで、ここでは違うアプローチをとることにします。
アプローチ1
\(2\) 次の行列式は列ベクトルに関して2重線形性や交代性のような性質をもつので、\(3\) 次の場合もそのような性質をもつものを見つけ出し、それを \(3\) 次の行列式と定義する。アプローチ2
\(2\) 次の行列式は列ベクトルで張られる平行四辺形の符号付き面積を与えるので、\(3\) 次の場合は列ベクトルで張られる平行六面体の符号付き体積を与えるものを見つけ出し、それを \(3\) 次の行列式と定義する。
それではそれぞれのアプローチで3次の行列式を発見したいと思いますが、以下 \(3\) 次の列ベクトルを \[\boldsymbol{a} = \left(\begin{array}{c}a_1\\a_2\\a_3\end{array}\right),\boldsymbol{b} = \left(\begin{array}{c}b_1\\b_2\\b_3\end{array}\right) ,\boldsymbol{c} = \left(\begin{array}{c}c_1\\c_2\\c_3\end{array}\right)\]
のように書くことにします。
アプローチ1にチャレンジ
発見しようとしている行列式 \(\det(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c})\) は、
3重線形性(つまり各列について線形)\[\begin{align} \det(\boldsymbol{a_1+a_2},\boldsymbol{b},\boldsymbol{c})&=\det(\boldsymbol{a_1},\boldsymbol{b},\boldsymbol{c})+\det(\boldsymbol{a_2},\boldsymbol{b},\boldsymbol{c})\\ \det(\boldsymbol{a},\boldsymbol{b_1+b_2},\boldsymbol{c})&=\det(\boldsymbol{a},\boldsymbol{b_1},\boldsymbol{c})+\det(\boldsymbol{a},\boldsymbol{b_2},\boldsymbol{c})\\ \det(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c_1+c_2})&=\det(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c_1})+\det(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c_2})\\ \det(r\boldsymbol{a},\boldsymbol{b},\boldsymbol{c})&=r\det(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c})\\ \det(\boldsymbol{a},r\boldsymbol{b},\boldsymbol{c})&=r\det(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c})\\ \det(\boldsymbol{a},\boldsymbol{b},r\boldsymbol{c})&=r\det(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c})\\ \end{align}\]
と交代性(どれか2つの列を入れかえると \(-1\)倍される) \[\begin{align} \det(\boldsymbol{b},\boldsymbol{a},\boldsymbol{c})&=-\det(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c})\\ \det(\boldsymbol{c},\boldsymbol{b},\boldsymbol{a})&=-\det(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c})\\ \det(\boldsymbol{a},\boldsymbol{c},\boldsymbol{b})&=-\det(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c})\\ \end{align}\] という性質を持っているというところから考えを進めます。
\(2\) 次のときと全く同じ考えで、交代性から直ちに、どれか2つの行ベクトルが等しいとき値は \(0\) になるということが導かれます。つまり、 \[\begin{align} \det(\boldsymbol{a},\boldsymbol{a},\boldsymbol{b})&=0\\ \det(\boldsymbol{a},\boldsymbol{b},\boldsymbol{a})&=0\\ \det(\boldsymbol{a},\boldsymbol{b},\boldsymbol{b})&=0\\ \end{align}\]
が成り立ちます。
ところで \(3\) 項単位ベクトル \[\boldsymbol{e}_1 = \left(\begin{array}{c}1\\0\\0\end{array}\right),\boldsymbol{e}_2 = \left(\begin{array}{c}0\\1\\0\end{array}\right) ,\boldsymbol{e}_3 = \left(\begin{array}{c}0\\0\\1\end{array}\right)\] を用いると、
\[\begin{align} \boldsymbol{a}&=a_1\boldsymbol{e}_1 +a_2\boldsymbol{e}_2 +a_3\boldsymbol{e}_3\\ \boldsymbol{b}&=b_1\boldsymbol{e}_1 +b_2\boldsymbol{e}_2 +b_3\boldsymbol{e}_3\\ \boldsymbol{c}&=c_1\boldsymbol{e}_1 +c_2\boldsymbol{e}_2 +c_3\boldsymbol{e}_3\\ \end{align}\] とあらわすことができます。
まず、3重線形性を用いると、\(\det\) は「展開のようなこと」ができるので、\[\begin{align} &\det(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c})\\ &=\det(a_1\boldsymbol{e}_1 +a_2\boldsymbol{e}_2 +a_3\boldsymbol{e}_3,b_1\boldsymbol{e}_1 +b_2\boldsymbol{e}_2 +b_3\boldsymbol{e}_3,c_1\boldsymbol{e}_1 +c_2\boldsymbol{e}_2 +c_3\boldsymbol{e}_3)\\ &=\mathrm{可能な}\, i,j,k\,\mathrm{の組すべてに対する} \,a_ib_jc_k\det(\boldsymbol{e}_i,\boldsymbol{e}_j,\boldsymbol{e}_k)\,\mathrm{の和} \end{align}\]
となります。
ここで、交代性を用いると、\(\boldsymbol{e}_i,\boldsymbol{e}_j,\boldsymbol{e}_k\) のどれか2つが同じならば \(\det(\boldsymbol{e}_i,\boldsymbol{e}_j,\boldsymbol{e}_k) = 0\) なので、\[\begin{align} &\det(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c})\\ &= i,j,k\,\mathrm{がすべて異なるときの},a_ib_jc_k\det(\boldsymbol{e}_i,\boldsymbol{e}_j,\boldsymbol{e}_k)\,\mathrm{の和}\\ &=a_1b_2c_3\det(\boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{e}_3)+a_1b_3c_2\det(\boldsymbol{e}_1,\boldsymbol{e}_3,\boldsymbol{e}_2)\\ &\quad+a_2b_1c_3\det(\boldsymbol{e}_2,\boldsymbol{e}_1,\boldsymbol{e}_3)+a_2b_3c_1\det(\boldsymbol{e}_2,\boldsymbol{e}_3,\boldsymbol{e}_1)\\ &\quad+a_3b_1c_2\det(\boldsymbol{e}_3,\boldsymbol{e}_1,\boldsymbol{e}_2)+a_3b_2c_1\det(\boldsymbol{e}_3,\boldsymbol{e}_2,\boldsymbol{e}_1)\\ \end{align}\]
となります。
再び交代性より、\(\det(\boldsymbol{e}_1,\boldsymbol{e}_3,\boldsymbol{e}_2 )=-\det(\boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{e}_3 )\) のようにして、すべての \(\det(\boldsymbol{e}_i,\boldsymbol{e}_j,\boldsymbol{e}_k )\) を適切な符号をつけて \(\pm\det(\boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{e}_3 )\) に替えられるので、\[\begin{align} &\det(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c})\\ &=(a_1b_2c_3 - a_1b_3c_2 - a_2b_1c_3 + a_2b_3c_1 + a_3b_1c_2-a_3b_2c_1)\det(\boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{e}_3)\\ \end{align}\]
となることがわかります。
ところで、\(2\) 次の行列の場合、\(\boldsymbol{e}_1=\left(\begin{array}{r}1\\0\end{array}\right),\boldsymbol{e}_2=\left(\begin{array}{r}0\\1\end{array}\right)\) に対して、\(\det(\boldsymbol{e}_1,\boldsymbol{e}_2)=\det\left(\begin{array}{r}1 & 0\\ 0&1\end{array}\right) =1\) となっていました。ですから、\(3\) 次の行列の場合も\[\det(\boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{e}_3)=1\]
が成り立つべきであるとしてしまうと都合が良いでしょう。
そうすると、\(3\) 次の列ベクトル\[\boldsymbol{a} = \left(\begin{array}{c}a_1\\a_2\\a_3\end{array}\right),\boldsymbol{b} = \left(\begin{array}{c}b_1\\b_2\\b_3\end{array}\right) ,\boldsymbol{c} = \left(\begin{array}{c}c_1\\c_2\\c_3\end{array}\right)\]
\[\det(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}) =a_1b_2c_3 - a_1b_3c_2 - a_2b_1c_3 + a_2b_3c_1 + a_3b_1c_2-a_3b_2c_1\]
と定義するのが良さそうです。
アプローチ2にチャレンジ
空間の場合に、平面の場合の平行四辺形に対応するものは平行六面体でしょう。
というわけで、まず空間に右手系の正規直交座標系を設けます。
そして、1つの平面に乗ることがなく零ベクトルとは異なる3つの幾何ベクトル \(\boldsymbol{a} = \left(\begin{array}{c}a_1\\a_2\\a_3\end{array}\right),\boldsymbol{b} = \left(\begin{array}{c}b_1\\b_2\\b_3\end{array}\right),\boldsymbol{c} = \left(\begin{array}{c}c_1\\c_2\\c_3\end{array}\right)\) によって張られる平行六面体の体積について考えることにします。このとき3つのベクトルは一次独立であることに注意しましょう。
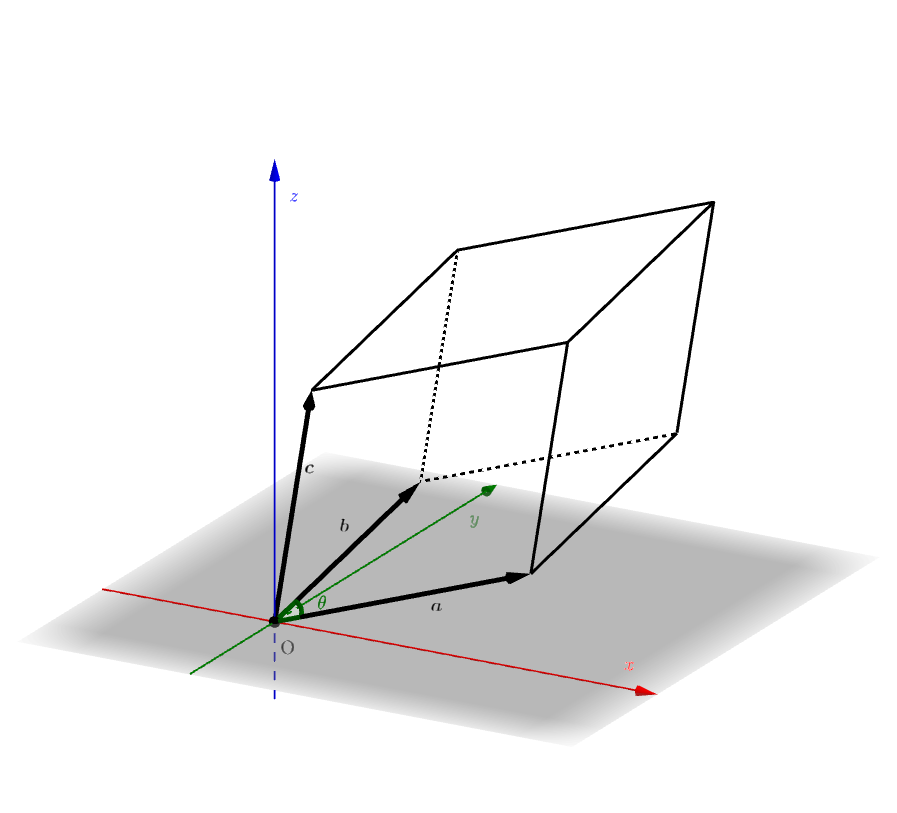
底面積の計算
\(\boldsymbol{a},\boldsymbol{b}\) で張られる平行四辺形を底面と考えることにし、その面積を \(S\) とあらわしておきます。 \(\boldsymbol{a},\boldsymbol{b}\) のなす角を \(\theta\)(ただし \(0 \lt\theta \lt \pi\))とすると、 \[\begin{align} S&=\|\boldsymbol{a}\|\|\boldsymbol{b}\|\sin\theta\\ &=\|\boldsymbol{a}\|\|\boldsymbol{b}\|\sqrt{1-\cos^2\theta}\\ &=\sqrt{\|\boldsymbol{a}\|^2\|\boldsymbol{b}\|^2-\|\boldsymbol{a}\|^2\|\boldsymbol{b}\|^2\cos^2\theta}\\ &=\sqrt{\|\boldsymbol{a}\|^2\|\boldsymbol{b}\|^2-(\boldsymbol{a}\cdot\boldsymbol{b}})^2\\ \end{align}\] となります。 これをさらに頑張って \(\boldsymbol{a},\boldsymbol{b}\) の成分を使って計算していくと、\[\begin{align} S&=\sqrt{(a_1^2+a_2^2+a_3^2)(b_1^2+b_2^2+b_3^2) -(a_1b_1+a_2b_2+a_3b_3)^2}\\ &=\sqrt{(a_2b_3-a_3b_2)^2+(a_3b_1-a_1b_3)^2+(a_1b_2-a_2b_1)^2} \end{align}\]
となることがわかります。
外積という概念の登場
次は平行六面体の高さについて考えます。そのために、\(\boldsymbol{a},\boldsymbol{b}\) 両方に垂直になるベクトルを見つけてみることにしましょう。
\(\boldsymbol{x}=\left(\begin{array}{c}x_1\\x_2\\x_3\end{array}\right)\) とおき、\(\boldsymbol{x}\) は \(\boldsymbol{a},\boldsymbol{b}\) 両方に垂直とすると、\(\boldsymbol{x}\cdot\boldsymbol{a}=0,\,\boldsymbol{x}\cdot\boldsymbol{b}=0\) が成り立つわけですから、\[\begin{align} a_1x_1 + a_2x_2 + a_3x_3&=0\tag{1}\\ b_1x_1 + b_2x_2 + b_3x_3&=0\tag{2}\\ \end{align}\]
が成り立ちます。
\((1),(2)\) 式から \(x_1\) を消去してみます。
\((1)\times b_1 -(2) \times a_1\) とすると、 \[\begin{align} a_1b_1x_1 + a_2b_1x_2 + a_3b_1x_3&=0\\ -)\quad a_1b_1x_1 + a_1b_2x_2 + a_1b_3x_3&=0\\ \hline (a_2b_1-a_1b_2)x_2+(a_3b_1-a_1b_3)x_3&=0 \end{align}\] つまり、 \[(a_1b_2-a_2b_1)x_2=(a_3b_1-a_1b_3)x_3\tag{3}\] となります。
同様にして、 \((1),(2)\) 式から \(x_2\) を消去すると、 \[(a_2b_3-a_3b_2)x_3=(a_1b_2-a_2b_1)x_1\tag{4}\] となり、 \((1),(2)\) 式から \(x_3\) を消去すると、 \[(a_3b_1-a_1b_3)x_1=(a_2b_3-a_3b_2)x_2\tag{5}\] となります。
\((3)\) を満たす \(x_2,x_3\) は \[\begin{align} x_2=k(a_3b_1-a_1b_3)\\ x_3=k(a_3b_1-a_1b_3) \end{align}, \;\mathrm{ただし}\, k\,\mathrm{は定数}\] とあらわすことができます。
また \((4)\) を満たす \(x_1,x_3\) は \[\begin{align} x_1=l(a_2b_3-a_3b_2)\\ x_3=l(a_1b_2-a_2b_1) \end{align}, \;\mathrm{ただし}\, l\,\mathrm{は定数}\] を採用することができますが、\(x_3\) を見比べて \(k=l\) としておきます。
このようにして得られる \(x_1,x_2,x_3\) が \((5)\) を満たすことは簡単に確認できます。
以上より、\(\boldsymbol{a},\boldsymbol{b}\) 両方に垂直なベクトル \(\boldsymbol{x}\) として、 \[\boldsymbol{x}=k\left(\begin{array}{c}a_2b_3-a_3b_2\\a_3b_1-a_1b_3\\a_1b_2-a_2b_1\end{array}\right),\;\mathrm{ただし}\, k\,\mathrm{は定数}\] を採用できることがわかりました。 \(k\) の符号を変えると \(\boldsymbol{x}\) の向きは正反対になることを頭に入れておきましょう。
この \(\boldsymbol{x}\) と先に求めた底面積 \(S\) の式を比べると、\(k=\pm 1\) のとき、\(S=\|\boldsymbol{x}\|\) であることがわかります。つまり、\(k = \pm 1\) のとき、今求めた \(\boldsymbol{x}\) は \(\boldsymbol{a},\boldsymbol{b}\) に垂直であるだけでなく、\(\boldsymbol{x}\) の長さは \(\boldsymbol{a},\boldsymbol{b}\) で張られる平行四辺形の面積になっているわけです。
実は、\(k=1\) の場合の \(\boldsymbol{x}\) の向きは 、\(\boldsymbol{a},\boldsymbol{b}\) が含まれる平面内で \(\boldsymbol{a}\) を \(\pi\, \mathrm{rad}\) までの角で回転して \(\boldsymbol{b}\) の方向を向かせるとき、右ねじの進む向きに一致します。つまり、\(\boldsymbol{a},\boldsymbol{b},\boldsymbol{x}\) の順でこれらは右手系になるということです。
このことは次のように考えると悟ることができます。 時間が進むに連れ、\(\boldsymbol{e}_1,\boldsymbol{e}_2\) が”連続的“に向きを変えたり、”連続的”に長さを変えながらそれぞれ \(\boldsymbol{a},\boldsymbol{b}\) に変化していく様子を頭の中で想像してみることにしましょう。そのために、時間 \(t\) によって変化する2つのベクトルを \(\boldsymbol{a}(t),\boldsymbol{b}(t)\) という記号であらわすことにし、 時間 \(t\) は \(0\) から \(T\) まで変化するとし、 \[\begin{align} \boldsymbol{a}(0) &= \boldsymbol{e}_1\\ \boldsymbol{b}(0) &= \boldsymbol{e}_2 \end{align}\]
\[\begin{align} \boldsymbol{a}(T) &= \boldsymbol{a}\\ \boldsymbol{b}(T) &= \boldsymbol{b} \end{align}\]
となっていると考えることにします。また、時間 \(t\) が進むに連れ、\(\boldsymbol{a}(t),\boldsymbol{b}(t)\) から作られる \(\boldsymbol{x}\) も変化していくのでそれをはっきりあらわすために、\(\boldsymbol{x}(t)\) と書くことにします。
変化する途中、\(\boldsymbol{a}(t)\) と \(\boldsymbol{b}(t)\) はどちらも決して \(\boldsymbol{0}\) にならず、決して平行にもならないようにできるのは頭の中に図を想像してみれば明らかでしょう。
そうすると、変化する途中、\(\boldsymbol{a}(t)\) と \(\boldsymbol{b}(t)\) で張られる平行四辺形の面積は \(0\) にはならないので \(\boldsymbol{x}(t)\) が \(\boldsymbol{0}\) になることもありません。
ところで、\(\boldsymbol{x}(0)\) は \(\boldsymbol{e}_1,\boldsymbol{e}_2\) から作られる \(\boldsymbol{x}\) なので、計算してみると \[\boldsymbol{x}(0) = \left(\begin{array}{c}0\\0\\1\end{array}\right)\] であることがわかります。ですから 時刻 \(t\) が \(0\) のとき、\(\boldsymbol{a}(0),\boldsymbol{b}(0),\boldsymbol{x}(0)\) はこの順に右手系になっています。 そして、時間 \(t\) が進むに連れ、\(\boldsymbol{a}(t),\boldsymbol{b}(t),\boldsymbol{x}(t)\) はこの順に右手系であることを保って変化していくはずです。 なぜなら、これは連続的に変化するので、途中のどこかで \(\boldsymbol{x}(t)\) が \(\boldsymbol{0}\) にならない限り、右手系から左手系に移ることはできないからです。 というわけで、 時刻 \(t\) が \(T\) のとき、\(\boldsymbol{a}(T),\boldsymbol{b}(T),\boldsymbol{x}(T)\) はこの順に右手系になっています。
以上の長い考察を受けて、次のように定義することにします。
定義
\(3\) 次の2つのベクトル \(\boldsymbol{a}= \left(\begin{array}{c}a_1\\a_2\\a_3\end{array}\right) ,\boldsymbol{b}=\left(\begin{array}{c}b_1\\b_2\\b_3\end{array}\right)\) に対し、 \[\left(\begin{array}{c}a_2b_3-a_3b_2\\a_3b_1-a_1b_3\\a_3b_1-a_1b_3\end{array}\right)\] として作られるベクトルを \(\boldsymbol{a},\boldsymbol{b}\) の外積と呼び、\(\boldsymbol{a}\times\boldsymbol{b}\) という記号であらわすことにします。
命題
上で定義された外積 \(\boldsymbol{a}\times\boldsymbol{b}\) は、これまでの考察からわかるように次の性質を持っています。
- \(\boldsymbol{a}\times\boldsymbol{b}\) の長さは \(\boldsymbol{a}\) と \(\boldsymbol{b}\) で張られる平行四辺形の面積に等しくなっています。
- \(\boldsymbol{a}\times\boldsymbol{b}\) は、\(\boldsymbol{a},\boldsymbol{b}\) に垂直です。
- \(\boldsymbol{a}\times\boldsymbol{b}\) の向きは、 \(\boldsymbol{a},\boldsymbol{b}\) が含まれる平面内で \(\boldsymbol{a}\) を \(\pi\, \mathrm{rad}\) までの角で回転して \(\boldsymbol{b}\) の方向を向かせるとき、右ねじの進む向きになります。
平行六面体の高さと体積
\(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}\) で張られる平行六面体の体積を \(V\) と書くことにします。
\(\boldsymbol{a}\times\boldsymbol{b}\) と平行六面体の3つ目の辺 \(\boldsymbol{c}\) のなす角を \(\phi\) とおきます。
高さの計算をわかりやすくするために \(\boldsymbol{a}\times\boldsymbol{b}\) と同じ向きの長さ \(1\) のベクトル \(\boldsymbol{n}\) を \[\boldsymbol{n}=\frac{\boldsymbol{a}\times\boldsymbol{b}}{\|\boldsymbol{a}\times\boldsymbol{b}\|}\] としておきます。
\(\boldsymbol{c}\) と \(\boldsymbol{a}\times\boldsymbol{b}\) が \(\boldsymbol{a}\) と \(\boldsymbol{b}\) で張られる平面に関して同じ側にある場合(つまり、\(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}\) の順で右手系になる場合)では
\[\begin{align}\mathrm{高さ} &= \|\boldsymbol{n}\|\|\boldsymbol{c}\|\cos\phi\\ &=\boldsymbol{n}\cdot\boldsymbol{c}\\ &=\frac{(\boldsymbol{a}\times\boldsymbol{b})\cdot\boldsymbol{c}}{\|\boldsymbol{a}\times\boldsymbol{b}\|} \end{align}\] となります。
よってこのとき体積 \(V\) は、 \[\begin{align} V &= S\times \frac{(\boldsymbol{a}\times\boldsymbol{b})\cdot\boldsymbol{c}}{\|\boldsymbol{a}\times\boldsymbol{b}\|}\\ &= \|\boldsymbol{a}\times\boldsymbol{b}\|\times \frac{(\boldsymbol{a}\times\boldsymbol{b})\cdot\boldsymbol{c}}{\|\boldsymbol{a}\times\boldsymbol{b}\|}\\ &=(\boldsymbol{a}\times\boldsymbol{b})\cdot\boldsymbol{c} \end{align}\] となります。
\(\boldsymbol{c}\) と \(\boldsymbol{a}\times\boldsymbol{b}\) が \(\boldsymbol{a}\) と \(\boldsymbol{b}\) で張られる平面に関して反対側にある場合(つまり、\(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}\) の順で左手系になる場合)では
\[\begin{align}\mathrm{高さ} &= \|\boldsymbol{n}\|\|\boldsymbol{c}\|\times(-\cos\phi)\\ &=-\boldsymbol{n}\cdot\boldsymbol{c}\\ &=-\frac{(\boldsymbol{a}\times\boldsymbol{b})\cdot\boldsymbol{c}}{\|\boldsymbol{a}\times\boldsymbol{b}\|}\end{align}\] となります。
よってこのとき体積 \(V\) は、 \[\begin{align} V &= S\times \left\{-\frac{(\boldsymbol{a}\times\boldsymbol{b})\cdot\boldsymbol{c}}{\|\boldsymbol{a}\times\boldsymbol{b}\|}\right\}\\ &= -\|\boldsymbol{a}\times\boldsymbol{b}\|\times \frac{(\boldsymbol{a}\times\boldsymbol{b})\cdot\boldsymbol{c}}{\|\boldsymbol{a}\times\boldsymbol{b}\|}\\ &=-(\boldsymbol{a}\times\boldsymbol{b})\cdot\boldsymbol{c} \end{align}\] となります。
\(3\) 次の場合の行列式を定義
列ベクトル \(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}\) で張られる平行六面体の符号付き体積を与えるものを見つけ出し、それを \(3\) 次の行列式と定義するのが良いと考えているのですから、
\[\det(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c})=(\boldsymbol{a}\times\boldsymbol{b})\cdot\boldsymbol{c}\] と定義すれば良さそうです。 これを成分であらわすと、\[\begin{align} \det(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c})&=(a_2b_3-a_3b_2)c_1 + (a_3b_1-a_1b_3)c_2 +(a_1b_2-a_2b_1)c_3\\ &=a_1b_2c_3 - a_1b_3c_2 - a_2b_1c_3 + a_2b_3c_1 + a_3b_1c_2-a_3b_2c_1 \end{align}\]
となります。
2つのアプローチの結果の比較
アプローチ1とアプローチ2の結論を見てみると同じであることがわかります。ですから、\(3\) 次の正方行列 \[\left(\begin{array}{c} a_1 & b_1 & c_1\\ a_2 & b_2 & c_2\\ a_3 & b_3 & c_3\\ \end{array}\right) =(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c})\] に対して、\[\det(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}) =a_1b_2c_3 - a_1b_3c_2 - a_2b_1c_3 + a_2b_3c_1 + a_3b_1c_2-a_3b_2c_1\]
と定義するのが良さそうだということになります。
ここで定義された \(3\) 次の行列式の性質
以上のように \(3\) 次の場合に行列式を定義しても、\(2\) 次の行列式が持っている性質と同様なものを持っていなければ、行列式と呼ぶにはふさわしくないかもしれません。すべてを確認するのは大変なので、ここでは、とりあえず
この \(3\) 次の行列式は行列の積を保つか?
行列で定まる一次変換を考えたとき、平行六面体の体積は符号付きで行列式倍になるのか?
ということを調べてみたいと思います。
行列式は行列の積を保つか?
2つの \(3\) 次の正方行列 \(A,B\) に対し、 \[\det(AB)=\det(A)\det(B)\] が成り立つことは、行列の成分を使い、地道に手間のかかる計算をすることにより確かめることができます。ぜひ自分の手をつかって計算してみてください。
行列で定まる一次変換を考えたとき、平行六面体の体積は符号付きで行列式倍になるのか?
\(3\) 次の正方行列 \(A\) は空間のベクトルの空間 \(V^3\) の一次変換を定めます。それは、\(V^3\) の幾何ベクトル \(\boldsymbol{x}\) を \(V^3\) の幾何ベクトル \(A\boldsymbol{x}\) に対応させる写像です。この一次変換を平行六面体の体積と関連付けてみます。
\(\boldsymbol{x},\boldsymbol{y},\boldsymbol{z}\) を \(V^3\) の 3つの幾何ベクトルとし、それらで張られる平行六面体の体積を \(V\) とし、\(A\boldsymbol{x},A\boldsymbol{y},A\boldsymbol{z}\) で張られる平行六面体の体積を \(V'\) とします。計算の見通しを良くするために 3つの行ベクトル \(\boldsymbol{x},\boldsymbol{y},\boldsymbol{z}\) を横に並べた正方行列 \(X\)、つまり、 \[X=(\boldsymbol{x},\boldsymbol{y},\boldsymbol{z})\] を準備しておきます。
すると、
\[AX=(A\boldsymbol{x},A\boldsymbol{y},A\boldsymbol{y})\] とあらわされます。
- \(A\) が右手系を右手系に写すとき \(\boldsymbol{x},\boldsymbol{y},\boldsymbol{z}\) と \(A\boldsymbol{x},A\boldsymbol{y},A\boldsymbol{z}\) は共に右手系か共に左手系です。このとき、
となることがわかります。
\[ V' =\pm \det(A\boldsymbol{x},A\boldsymbol{y},A\boldsymbol{z}) =\pm\det(AX) =\pm \det(A)\det(X)=\det(A)\cdot\{\pm\det(\boldsymbol{x},\boldsymbol{y},\boldsymbol{z})\}=\det(A)V\]
- \(A\) が右手系を左手系に写すとき \(\boldsymbol{x},\boldsymbol{y},\boldsymbol{z}\) と \(A\boldsymbol{x},A\boldsymbol{y},A\boldsymbol{z}\) はどちらか一方が右手系でもう一方は左手系です。 このとき、
となることがわかります。
\[V' =\pm \det(A\boldsymbol{x},A\boldsymbol{y},A\boldsymbol{z}) =\pm\det(AX) =\pm \det(A)\det(X)=-\det(A)\cdot\{\mp\det(\boldsymbol{x},\boldsymbol{y},\boldsymbol{z})\}=-\det(A)V \]
以上より、\(A\) が右手系を右手系に移すとき、平行六面体の体積は \(\det(A)\)倍になり、\(A\) が右手系を左手系に移すとき、平行六面体の体積は \(-\det(A)\)倍になるということがわかりました。
まとめ
\(2\) 次の正方行列 \(A=\left(\begin{array}{c}a & b\\c & d\end{array}\right)\) が逆行列をもつのはどんなときなのかを調べてみると \(ad-bc\) が \(0\) とは異なる値になるときであることがわかりました。そしてこの値を \(2\) 次の正方行列の行列式と呼ぶことにしました。
\(2\) 次の正方行列の行列式は2重線型性や交代性と呼ばれる性質を持っていることがわかりました。
\(2\) 次の正方行列の行列式の値は、行列の各列を構成している2つの列ベクトルを直交座標系の平面幾何ベクトルだと考えた場合、それらによって張られる平行四辺形の面積に等しいか、面積のマイナス \(1\) 倍になっていることがわかりました。
\(2\) 次の正方行列を平面ベクトルの一次変換と考えた場合、この変換はどんな平行四辺形の面積もこの行列の「行列式倍」または「マイナス行列式倍」にするということがわかりました。
\(2\) 次の正方行列の行列式に関する以上の考察から、3次の正方行列に対しても
- 2重線型性や交代性を持つもの
- 平行六面体の体積を与えるもの
を見つけてみると
\(\left(\begin{array}{c}a_1 & b_1 & c_1\\ a_2 & b_2 & c_2 \\ a_3 & b_3 &c_3 \end{array}\right)\) に対して
\[\begin{align} a_1b_2c_3 - a_1b_3c_2 - a_2b_1c_3 + a_2b_3c_1 + a_3b_1c_2-a_3b_2c_1 \end{align}\]
のようにして計算されるものが見つかりました。そこでこれを \(3\) 次の正方行列の行列式と呼ぶことにしました。
このようにして見つかった \(3\) 次の行列の行列式は、\(2\) 次の場合と同じように、「積を保つ」という性質を持ち、「平行六面体の体積を行列式倍またはマイナス行列式倍」するということが確かめられました。
ところで、このようにして見つけられた \(3\) 次の場合の行列式は、逆行列の存在を判定することができるのでしょうか?