行列式の計算例
2022-10-15
これまでに「行列式の定義と性質」や「行列式の展開」について説明してきました。
ところで、行列の次数が大きくなると、行列式の計算はとても手間のかかるものになります。ここでは例を通じて、行列式を計算する際の基本的な方針について考えてみることにします。
定義から直接計算
まず行列式の定義を思い出しておきます。 \(n\) 次の正方行列 \(A=\left( \begin{array}{cccc} a_{ 11 } & a_{ 12 } & \ldots & a_{ 1n } \\ a_{ 21 } & a_{ 22 } & \ldots & a_{ 2n } \\ \vdots & \vdots & \ddots & \vdots \\ a_{ n1 } & a_{ n2 } & \ldots & a_{ nn } \end{array} \right)\) に対して、
\[|A|=\sum_{\sigma \in S_n}\mathrm{sgn}(\sigma)a_{1\sigma(1)}a_{2\sigma(2)}\cdots a_{n\sigma(n)} \tag{1}\\ \qquad\text{ただしここで}\, S_n \,\text{は}\,n\,\text{次の置換の集合}\]
として作られる数 \(|A|\) を \(A\) の行列式と定義したのでした。
それではここで、この定義式を使って直接計算する例をいくつか紹介します。
例
\(2\) 次と \(3\) 次の行列の行列式
定義に従ってすべての項をつくることにより \(2\) 次の行列の行列式は\[ \left|\begin{array}{cc} a_{11} & a_{12}\\ a_{21} & a_{22} \end{array}\right| =a_{11}a_{22}-a_{12}a_{21} \]
\[ \begin{align} \left|\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\\ \end{array}\right| &=a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{31}\\ &\qquad - a_{11}a_{23}a_{31}+a_{12}a_{21}a_{33}+a_{13}a_{22}a_{31} \end{align} \]
となることがわかります。
\(2\) 次や \(3\) 次の行列式だけに適用できる割とわかりやすい覚え方があります。もう一度上の計算結果を見ると、実は次の図のように計算していることになります。
\(2\) 次の場合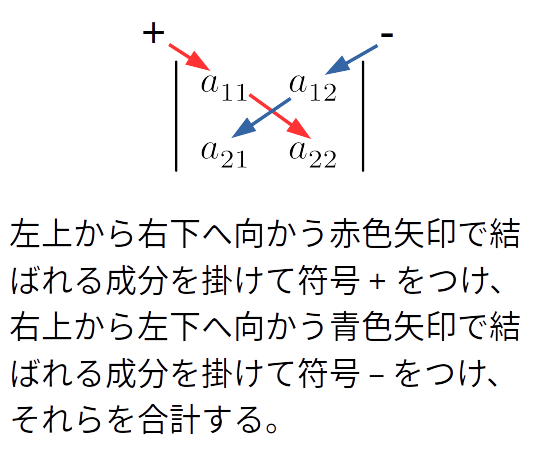
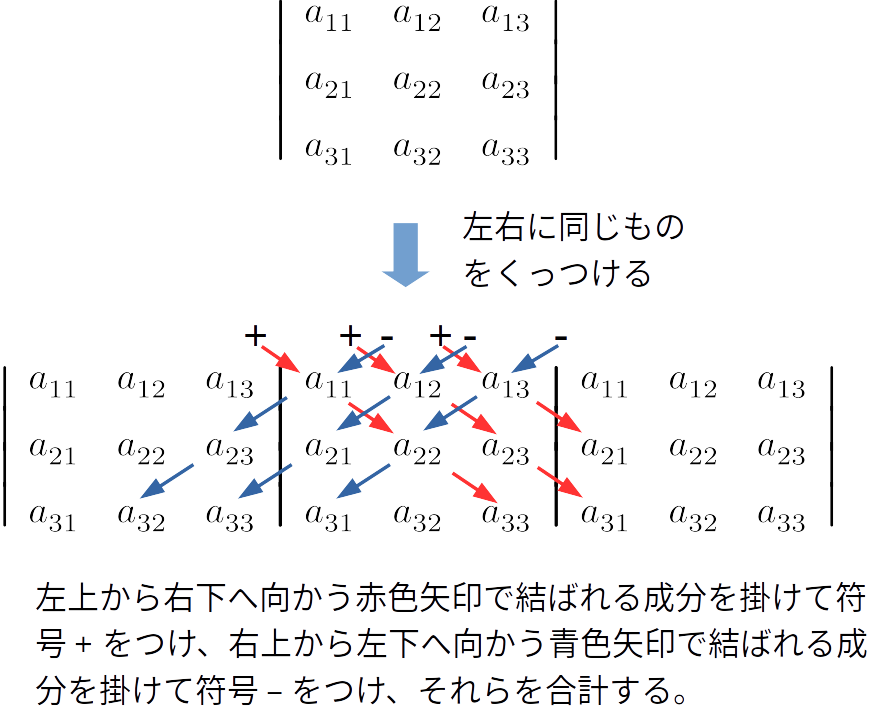
これらはたすきがけの規則と呼ばれることがあります。また、\(3\) 次のものはサラスの規則と呼ばれることもあるようです。
\(4\) 次以上の場合、このようなわかりやすい覚え方はありません。
例
対角行列の行列式
行列式の定義 \((1)\) 式に現れる項のうち、\(0\) にならないものは \(\sigma =\left(\begin{array}{cccc}1 & 2 & \cdots & n\\ 1 & 2 & \cdots & n \end{array}\right)\) に対応する項だけであることに注意すると、\[ \left|\begin{array}{cccc} a_{11} & 0 & \cdots & 0\\ 0 & a_{22} & \cdots & 0\\ \vdots & \vdots &\ddots & \vdots\\ 0 & 0 & \cdots & a_{nn}\\ \end{array}\right| =a_{11}a_{22} \cdots a_{nn} \]
となることがわかります。
例
上三角行列の行列式
対角行列の場合と同じく、行列式の定義に現れる項のうち、\(0\) にならないものは \(\sigma =\left(\begin{array}{cccc}1 & 2 & \cdots & n\\ 1 & 2 & \cdots & n \end{array}\right)\) に対応する項だけであることに注意すると、
\[ \left|\begin{array}{cccc} a_{11} & a_{12} & \cdots & a_{1n}\\ 0 & a_{22} & \cdots & a_{2n}\\ \vdots & \vdots &\ddots & \vdots\\ 0 & 0 & \cdots & a_{nn}\\ \end{array}\right| =a_{11}a_{22} \cdots a_{nn} \]
となることがわかります。
例
ある列がすべて \(0\) である行列の行列式 では\[ \left| \begin{array}{ccccc} a_{ 11 } & \ldots & 0 & \ldots & a_{ 1n } \\ a_{ 21 } & \ldots & 0 & \ldots & a_{ 2n } \\ \vdots & & \vdots & & \vdots \\ a_{ n1 } & \ldots & 0 & \ldots & a_{ nn } \end{array} \right|=0 \]
が成り立ちます。
なぜなら、\(\sigma\) がどんな置換でも \(a_{1\sigma(1)},a_{2\sigma(2)},\ldots,a_{n\sigma(n)}\) のどれかは必ず \(0\) になり、行列式の定義に現れる項はすべて \(0\) となるからです。
例
ある行列を定数倍した行列の行列式では
\[ \left| \begin{array}{cccc} ca_{ 11 } & ca_{ 12 } & \ldots & ca_{ 1n } \\ ca_{ 21 } & ca_{ 22 } & \ldots & ca_{ 2n } \\ \vdots & \vdots & \ddots & \vdots \\ ca_{ n1 } & ca_{ n2 } & \ldots & ca_{ nn } \end{array}\right| = c^n \left| \begin{array}{cccc} a_{ 11 } & a_{ 12 } & \ldots & a_{ 1n } \\ a_{ 21 } & a_{ 22 } & \ldots & a_{ 2n } \\ \vdots & \vdots & \ddots & \vdots \\ a_{ n1 } & a_{ n2 } & \ldots & a_{ nn } \end{array} \right| \]
が成り立ちます。
ある行列を \(c\) 倍した行列では、\(\sigma\) がどんな置換でも \(a_{1\sigma(1)},a_{2\sigma(2)},\ldots,a_{n\sigma(n)}\) のすべてが \(c\) 倍されます。ですから、行列式の定義に現れる項はすべて \(c^n\) 倍され、行列式も \(c^n\) 倍されるわけです。
区分けによる計算
例
正方行列 \(A\) を 適切に区分けして、\[ \begin{align} A&=\left(\begin{array}{cc} A_{11} & O\\ A_{21} & A_{22} \end{array}\right)\\[6pt] &\quad \text{ただし、ここで} \,A_{11}\, \text{と} \,A_{22}\, \text{は}\\ &\quad \text{それぞれある次数の正方行列} \end{align} \]
\[ |A|=|A_{11}||A_{22}| \]
が成り立ちます。
証明
行列の成分で書いてみると\[|A|=\left| \begin{array}{cccccc} a_{ 11 } &\ldots & a_{ 1m } & 0 &\ldots & 0 \\ \vdots & & \vdots & \vdots & & 0\\ a_{ m1 } & \ldots & a_{mm} &0 &\ldots & 0 \\ a_{ m+1\,1 } & \ldots & a_{m+1\,m} &a_{m+1\,m+1} &\ldots & a_{m+1\,m+n} \\ \vdots & \vdots & \ddots & \vdots & & \vdots \\ a_{ m+n\,1 } & \ldots & a_{m+n\,m} & a_{m+n\, m+1} &\ldots & a_{ m+n\,m+n } \end{array} \right|,\,\\[20pt] |A_{12}|=\left| \begin{array}{ccc} a_{ 11 } &\ldots & a_{ 1m } \\ \vdots & & \vdots \\ a_{ m1 } & \ldots & a_{mm} \\ \end{array} \right|,\quad |A_{22}|=\left| \begin{array}{ccc} a_{m+1\,m+1} &\ldots & a_{m+1\,m+n} \\ \vdots & & \vdots \\ a_{m+n\, m+1} &\ldots & a_{ m+n\,m+n } \end{array} \right|\]
\[\sigma =\left(\begin{array}{cccc}1 & \cdots & m & m+1 & \cdots & m+n\\ \sigma(1) & \cdots & \sigma(m) & \sigma(m+1) & \cdots & \sigma(m+n) \end{array}\right)\]
において、\(\sigma(1),\sigma(2),\ldots,\sigma(m)\) のどれか1つでも \(1,2,\ldots,m\) 以外の数になると \(a_{1\sigma(1)},a_{2\sigma(2)},\ldots,a_{m\sigma(m)}\) の少なくともどれか1つは \(0\) になるので、その \(\sigma\) に対応する項 \(a_{1\sigma(1)}a_{2\sigma(2)}\cdots a_{m+n\,\sigma(m+n)}\) は \(0\) となります。
ですから、\(|A|\) を定義に従って計算する際、置換 \(\sigma\) として \(1,2,\ldots,m\) を \(1,2,\ldots,m\) の中で並べ替え、 \(m+1,m+2,\ldots,m+n\) を \(m+1,m+2,\ldots,m+n\) の中で並べ替えるようなものだけを考えれば良いことになります。
そのような \(\sigma\) は 文字 \(1,2,\ldots,m\) に関する \(m\) 次の置換 \(\tau\) と 文字 \(m+1,m+2,\ldots,m+n\) に関する \(n\) 次の置換 \(\rho\) の組合せと考えることができ、そのように考えるとき(\(\sigma\) の転移は \(\tau\) と \(\rho\) にまたがるものはないから ) \(\mathrm{sgn}(\sigma)=\mathrm{sgn}(\tau)\mathrm{sgn}(\rho)\) が成り立つので、\(|A|\) の定義に現れる \(\sigma\) に対応する項は
\[ \mathrm{sgn}(\tau)\mathrm{sgn}(\rho)\left(a_{1\tau(1)}\cdots a_{m\tau(m)}\cdot a_{m+1\,\rho(m+1)}\ldots a_{m+n\,\rho(m+n)}\right) \]
となります。
これより、\[ \begin{align} |A|&=\sum_{(\tau,\rho)}\left\{\mathrm{sgn}(\tau)\mathrm{sgn}(\rho)\left(a_{1\tau(1)}\cdots a_{m\tau(m)}\cdot a_{m+1\,\rho(m+1)}\ldots a_{m+n\,\rho(m+n)}\right)\right\}\\ &=\sum_{\tau}\sum_{\rho}\left\{\left(\mathrm{sgn}(\tau)a_{1\tau(1)}\cdots a_{m\tau(m)}\right)\cdot\left(\mathrm{sgn}(\rho) a_{m+1\,\rho(m+1)}\ldots a_{m+n\,\rho(m+n)}\right)\right\}\\ &=\sum_{\tau}\mathrm{sgn}(\tau)a_{1\tau(1)}\cdots a_{m\tau(m)}\cdot\sum_{\rho}\mathrm{sgn}(\rho) a_{m+1\,\rho(m+1)}\ldots a_{m+n\,\rho(m+n)}\\ &=|A_{11}||A_{22}| \end{align} \]
行列式の展開を利用する計算
むやみに行または列を選んで展開する前に、展開に利用するつもりの行または列にほかの行または列のナントカ倍を足すなどして、展開に利用するつもりの行または列になるべく多く \(0\) をつくるようにするのが良いでしょう。
例
次の計算では第 \(2\) 行の一番左の数以外をすべて \(0\) にしてから展開をおこなっています。
\[ \begin{align} \left|\begin{array}{rrrr} -2 & 2 & 1& 2 \\ 1 & 0 & 4 & -4 \\ 3 & -5 & 2 & -9 \\ 4 & 1& -7 & 3 \end{array} \right| &\stackrel{3\text{列}+4\text{列}\times 1\,}{=} \left|\begin{array}{rrrr} -2 & 2 & 3 & 2 \\ 1 & 0 & 0 & -4 \\ 3 & -5 & -7 & -9 \\ 4 & 1& -4 & 3 \end{array} \right|\\[15pt] &\stackrel{4\text{列}+1\text{列}\times 4\,}{=} \left|\begin{array}{rrrr} -2 & 2 & 3& -6 \\ 1 & 0 & 0 & 0 \\ 3 & -5 & -7 & 3 \\ 4 & 1& -4 & 19 \end{array} \right|\\[15pt] &\stackrel{\text{第}\,2\,\text{行で展開}}{=} 1\times(-1)^{2+1}\left|\begin{array}{rrr} 2 & 3& -6 \\ -5 & -7 & 3 \\ 1& -4 & 19 \end{array} \right| + 0\times (-1)^{2+2}\left|\begin{array}{rrr} * & * & *\\ * & * & * \\ * & * & *\\ \end{array} \right|\\[15pt] & \qquad \qquad \qquad+ 0 \times (-1)^{2+3} \left|\begin{array}{rrr} * & * & *\\ * & * & * \\ * & * & *\\ \end{array} \right| + 0\times (-1)^{2+4} \left|\begin{array}{rrr} * & * & *\\ * & * & * \\ * & * & *\\ \end{array} \right|\\[15pt] &\quad=\quad (-1)\times \left|\begin{array}{rrr} 2 & 3& -6 \\ -5 & -7 & 3 \\ 1& -4 & 19 \end{array} \right|\\[15pt] &\stackrel{1\text{行}-3\text{行}\times 2\,}{=}(-1)\times \left|\begin{array}{rrr} 0 & 11 & -44 \\ -5 & -7 & 3 \\ 1& -4 & 19 \end{array} \right|\\ &\stackrel{2\text{行}+3\text{行}\times 5\,}{=}(-1)\times \left|\begin{array}{rrr} 0 & 11 & -44 \\ 0 & -27 & 98 \\ 1& -4 & 19\\ \end{array} \right|\\[15pt] &\stackrel{\text{第}\,1\,\text{列で展開}}{=} (-1)\times\left\{0\times(-1)^{1+1}\times \left|\begin{array}{rr} * & * \\ * & * \end{array} \right|\right.\\[15pt] &\qquad\qquad\qquad\qquad\qquad\qquad\left.+0\times (-1)^{2+1}\times \left|\begin{array}{rr} * & * \\ * & * \end{array} \right|\right.\\[15pt] &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\left.+1\times (-1)^{3+1}\times \left|\begin{array}{rr} 11 & -44 \\ -27 & 98 \\ \end{array} \right|\right\}\\[15pt] &\quad = \quad -1\times\left\{11\times74-(-44)\times(-9)\right\}=-1\times (-110) =110 \end{align} \]
この計算中で、\(\left|\begin{array}{rrr} * & * & *\\ * & * & * \\ * & * & *\\ \end{array}\right|\) のように書かれているものは、展開により \(0\) と掛け算されて消えてしまうものです。ですから、実際に計算する時に、このような項をわざわざ書く必要はありません。
まとめ
一般に、行列式の計算を定義に従っておこなうのが得策なのは \(2\) 次や \(3\) 次までの場合で、\(4\) 次以上になると何らかの工夫を必要とします。
上三角行列や対角行列のように、特殊な形をしている行列式は計算が簡単です。
行と列に関して対称な区分けにより、右上または左下のブロックが \(\boldsymbol{0}\) になっているような行列の場合、行列式の計算は小さい次数の行列式の積として計算できます。
一般には 、行列式の値が変わらないような変形を使い、\(0\) が都合よく並ぶように、\(0\) をなるべく多くつくってから展開をして次数を下げて行くことがポイントになります。