平面や空間の座標系
2022-05-06
座標系
平面や空間に座標系と呼ばれるものを設定すると、点を数の組であらわすことができます。そのような数の組は、点の座標と呼ばれます。これから、平面の場合と空間の場合に分けて説明していきます。
平面の座標系
平面のどこかに原点と呼ばれる点 \(\mathrm{O}\) を設け、\(\mathrm{O}\) で交わり平行ではない2つの向きのついた直線を描きます。 この2つの直線は軸と呼ばれます。
ここでは、この2本の直線をそれぞれ \(x\) 軸、\(y\) 軸と呼ぶことにします。また、\(x\) 軸、\(y\) 軸は必ずしも直交していなくても構いません。 そして、それぞれの直線にそれぞれ単位となる長さを決め目盛りをつけます。
このようなものを、平面の座標系といいます。
注意:2つの軸は直角に交わっていなくても構いません。 また、2つの軸の単位の長さは違っていても構いませんが、 それぞれの軸では目盛りは等間隔につけるようにします。
このような座標系を使うとこれから説明するように、平面上のどの点にも2つの数の組を対応させることができます。
\(\mathrm{P}\) を平面の点とします。 \(\mathrm{P}\) を通り \(y\) 軸に平行な直線を考えてみると、この直線と \(x\) 軸はある場所で交わるはずです。そしてその交点で \(x\) 軸の目盛りを読み取ります。 たとえば次の図では \(x\) 軸の目盛りを読み取ると \(2\) になります。
同様にして、\(\mathrm{P}\) を通り \(x\) 軸に平行な直線と \(y\) 軸との交点の目盛りを読み取ります。たとえばこの図では \(y\) 軸の目盛りを読み取ると \(3\) になります。
以上のようにして2つの数 \(2\) と \(3\) が得られますがそれらを 縦に並べカッコでくくり、\(\left( \begin{array}{r} 2\\ 3 \end{array} \right)\) のようにあらわします。
つまり、一般に、点 \(\mathrm{P}\) に対して今説明したようにして読み取られた数が \(x\) と \(y\) であるとき、次のようにこれら2つの数を縦に並べ、カッコでくくるわけです。
\[\left( \begin{array}{r} x\\ y \end{array} \right)\]
このようにして得られるものを平面の点 \(\mathrm{P}\) の座標といいます。
空間の座標系
空間の場合も平面と同様に考えることできます。
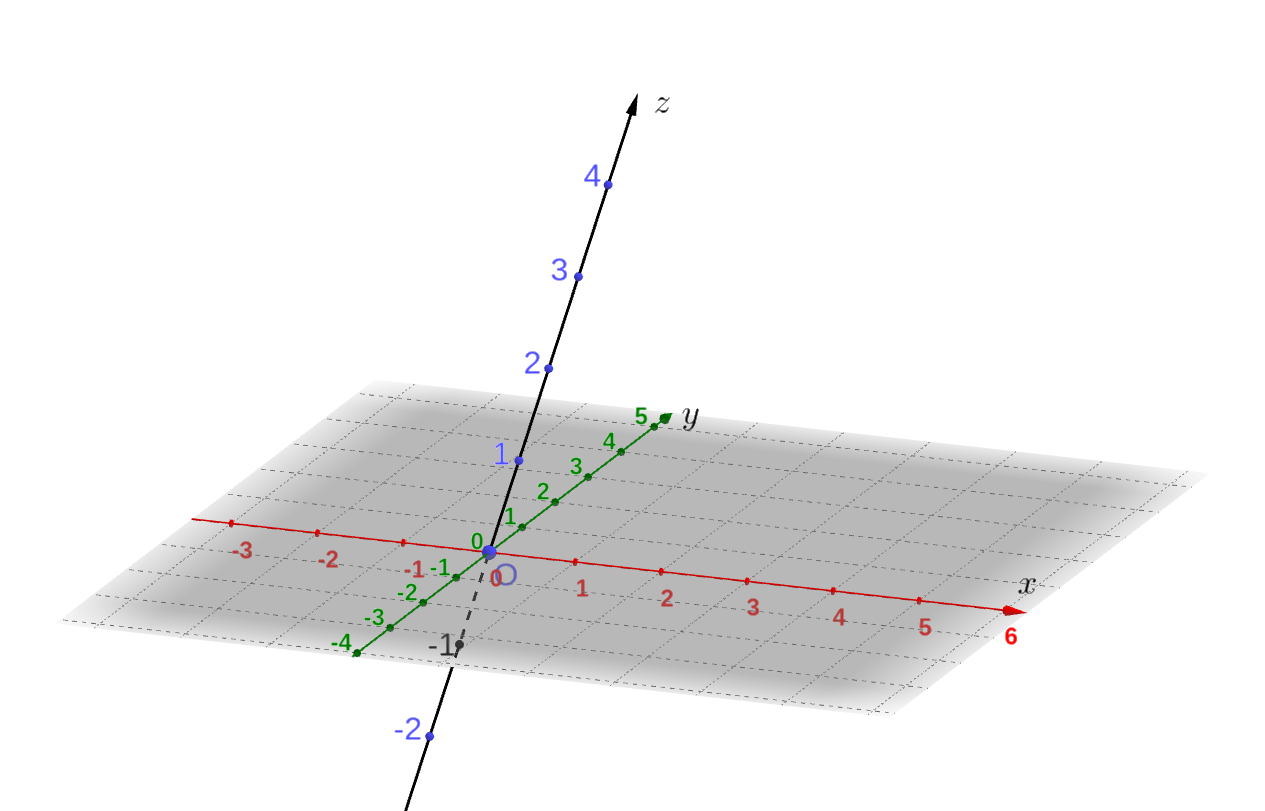
空間のどこかに原点 \(\mathrm{O}\) を設け、\(\mathrm{O}\) で交わる向きのついた3本の直線を描きます。ただし、3本の直線の全部がある1つ平面に含まれてしまわないようにします。そして、それぞれの直線にそれぞれ単位となる長さを決め目盛りをつけます。
ここでは、この3本の直線を \(x\) 軸、\(y\) 軸、\(z\) 軸と呼ぶことにします。 また、\(x\) 軸、\(y\) 軸、\(z\) 軸は必ずしも直交していなくても構いません。
このようすると、空間に1つ座標系を設けることができます。
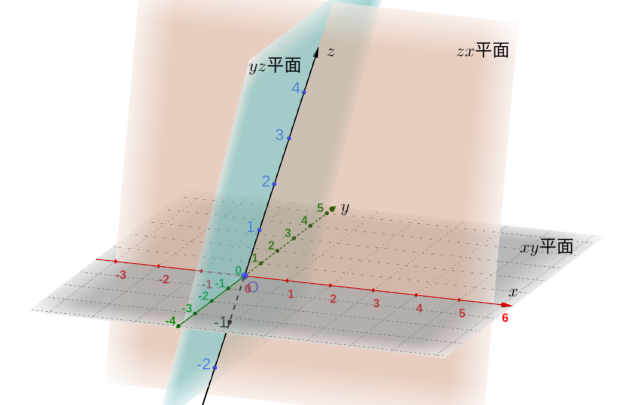
\(y\) 軸と \(z\) 軸を含む平面を \(yz\) 平面、\(z\) 軸と \(x\) 軸を含む平面を \(zx\) 平面、\(x\) 軸と \(y\) 軸を含む平面を \(xy\) 平面と呼ぶことにします。
この座標系を使うと、これから説明するように、平面の場合と同じようにして、空間のどの点にも3つの数の組を対応させることができます。
\(\mathrm{P}\) を空間の点とします。そして \(\mathrm{P}\) を通り \(yz\) 平面に平行な平面を考えます。この平面と \(x\) 軸はある場所で交わるはずですから、交点で \(x\) 軸の目盛りを読み取ります。たとえば次の図では、交点の座標を読み取ると \(2\) になります。

同様にして、\(\mathrm{P}\) を通り \(zx\) 平面に平行な平面と \(y\) 軸との交点の目盛りを読み取り、さらに \(\mathrm{P}\) を通り \(xy\) 平面に平行な平面と \(z\) 軸との交点の目盛りを読み取ります。
このようにすると3つの数が得られますがここではそれらを \(x,y,z\) であらわすことにします。そして次のように、これら3つの数を縦に並べ、カッコでくくります。
\[ \left( \begin{array}{r} x\\ y\\ z \end{array} \right) \]
このようにして得られるものを 空間の点 \(\mathrm{P}\) の座標といいます。
注意:3つの軸は直角に交わっていなくても構いません。 また、3つの軸の単位の長さは違っていても構いませんが、それぞれの軸では目盛りは等間隔につけられていなければなりません。
直交座標系
平面の場合でも、空間の場合でも、軸が原点 \(\mathrm{O}\) で直角に交わるような座標系を直交座標系といいます。
そして特に、すべての軸で単位の長さ(つまり1目盛りの長さ)が同じになっている直交座標系を正規直交座標系といいます。
右手系と左手系
平面の場合でも空間の場合でも本質的に区別できる2つの直交座標系があります。これらはそれぞれ右手系の直交座標系、左手系の直交座標系と呼ばれます。
平面の場合
- 右手系
\(\mathrm{O}\) を中心に \(x\) 軸を反時計回りに回転していくと \(y\) 軸に重なります。 - 左手系
\(\mathrm{O}\) を中心に \(x\) 軸を時計回りに回転していくと \(y\) 軸に重なります。
空間の場合
\(z\) 軸の真上から見ているときのことを想像してください。
- 右手系
\(z\) 軸を軸として反時計回りに回転すると、\(x\) 軸が \(y\) 軸に重なります。 - 左手系
\(z\) 軸を軸として時計回りに回転すると、\(x\) 軸が \(y\) 軸に重なります。
補足:右手系、左手系という概念は必ずしも直交していない座標系に対しても同じようにして考えることができます。
座標の変換
平面や空間のなかに座標系を設定する仕方はいくらでもあります。そして、座標系を異なるものに取り替えると、点の座標も変わります。そのことを平面の座標の例で見てみます。
次の図は、平面に座標系 1(緑色)と座標系 2(赤色)を描いたものです。
座標系 1(緑色)の2つの軸を \(x\) 軸 、\(y\) 軸と呼ぶことにし、座標系 2(赤色)の2つの軸を \(x'\) 軸 、\(y'\) 軸と呼ぶことにします。
この図では、座標系 2(赤色)の \(x'\) 軸は座標系 1(緑色)では直線 \(\displaystyle y=\frac14x\) であらわされるものにしてあり、座標系 2 の \(y'\) 軸は座標系 1(緑色)では直線 \(y=2x\) であらわされるものにしてあります。
また、座標系 2(赤色)の \(x'\) 軸上と \(y'\) 軸上にそれぞれ点 \(\mathrm{A'},\mathrm{B'}\) がありますが、これらの点は座標系 1(緑色) で \(\left(\begin{array}{r}4\\ 1 \end{array}\right), \left(\begin{array}{r} 1\\ 2 \end{array} \right)\) という座標をもつものです。
そして座標系 2(赤色)では、\(\mathrm{O}\) から \(\mathrm{A'}\) までの長さを \(x'\) 軸の単位の長さとし、\(\mathrm{O}\) から \(\mathrm{B'}\) までの長さを \(y'\) 軸の単位の長さとして目盛りをつけてあります。
点の座標を座標系 1(緑色)で読み取ったものと座標系 2(赤色)で読み取ったものは異なります。
例えばこの図の点 \(\mathrm{P}\) は、座標系 1(緑色)では \(\left(\begin{array}{c} 11\\ 8 \end{array} \right)\)、座標系 2 (赤色)では \(\left( \begin{array}{r} 2\\3 \end{array}\right)\) であらわされます。
さらに一生懸命考えると、平面のどの点 \(\mathrm{P}\) に対しても、座標系 1(緑色) で読み取った座標 \(\left(\begin{array}{r} x\\ y \end{array} \right)\) と、座標系 2(赤色) で読み取った座標 \(\left( \begin{array}{r} x'\\ y' \end{array} \right)\) の間には
\[ \left\{ \begin{align} &x'= \frac27x-\frac17y \\ &y'= -\frac17x+\frac47y \end{align} \right. \]
という関係、つまり行列で書けば
\[ \left( \begin{array}{r} x'\\ y' \end{array} \right) = \left(\begin{array}{r} \frac27 & -\frac17 \\ -\frac17 & \frac47 \end{array}\right) \left( \begin{array}{r} x\\ y \end{array} \right) \]
という関係があることがわかります。どうしてこのような関係式が成り立つのかは各自で考え計算してみてください。
座標系を取り替えると座標がどのように変るのかということを調べることは、線形代数学の大切なテーマの1つです。 線形代数学では、このようなことをベクトルの概念を使って議論します。 そして、そのような議論を進めていくと、ベクトル空間の基底と呼ばれる概念を見つけることにつながり、それは座標系の代わりの役目を果たすことになります。
注意:ここでは、直線の軸をもつ座標系の話をしました。しかし、曲線からなる座標系を導入することもできます。その代表的なものに次の図のようなものがあり、「極座標」と呼ばれています。
極座標では、点の位置を「原点からの距離」と「\(x\) 軸の正の方向から反時計回りにどれぐらい回転しているのか」という2つの数を組にしてあらわします。たとえば、この図の点 \(\mathrm{P}\) の座標は \((3, \pi/6)\) とあらわされます。
線形代数学では、原則として、直線からなる座標系を考えます。 直線からなる座標系はベクトルと相性が良いからです。
まとめ
平面や空間に座標系と呼ばれるものを設定すると、点を数の組であらわすことができ、そのような数の組は点の座標と呼ばれます。
座標系を構成する「軸」は必ずしも直角に交わる必要はなく、それぞれの「軸」の単位の長さは違っていても構いません。
軸が直角に交わるような座標系を直交座標系といい、すべての軸で単位の長さが同じになっているような直交座標系を正規直交座標系といいます。
座標系には右手系と呼ばれるものと左手系と呼ばれるものがあります。
平面や空間のなかに座標系を設定する仕方はいくらでもあり、座標系を異なるものに取り替えると、点の座標も変わります。