平面や空間のベクトル

2022-05-04

矢印であらわされるベクトル

平面や空間内に矢印が描かれているのを想像してみてください。この時、その矢印のことをベクトルといいます。

ただし、向きと長さの同じ矢印は区別しないで同じものとして考えることにします。ですから、2つの矢印があり、片方の矢印を平行移動した時にもう片方の矢印にぴったり重なるなら、その2つの矢印はベクトルとしては同じものです。

この説明からわかるように、厳密には、ベクトルは「矢印そのもの」ではありませんが、「矢印から向きと長さというものを抜き出した概念」ということになります。 そして、矢印はベクトルを図示するために使われ、ベクトルを代表しているということになります。
ですから、向きと長さを変えずに、好きなところに矢印を平行移動してもベクトルとしては同じものです。

ベクトルは「どっちの方向に、どのぐらい移動するのかということを矢印であらわしたもの」と考えることもできます。

ベクトルをあらわす記号

矢印には「始点」と「終点」があります。
たとえば、矢印の始点に \(\mathrm{A}\)、終点に \(\mathrm{B}\) という名前をつけることにすると、この矢印は \(\mathrm{A}\) から \(\mathrm{B}\) へ向かっているので \(\overrightarrow{\mathrm{A}\mathrm{B}}\) という記号であらわすのが良いでしょう。
ところで、いま、別の場所に \(\mathrm{C}\) から \(\mathrm{D}\) へ向かう矢印 \(\overrightarrow{\mathrm{C}\mathrm{D}}\)があり、これは \(\overrightarrow{\mathrm{A}\mathrm{B}}\) と同じ向きで同じ長さを持っているとします。
下の図を見てください。
ベクトルという言葉を使う時は向きと長さの同じ矢印は区別しないので\(\overrightarrow{\mathrm{A}\mathrm{B}}\) と \(\overrightarrow{\mathrm{C}\mathrm{D}}\) はベクトルとしては同じものです。

ベクトルをあらわす時にいつでも始点や終点を書くのは面倒であったり、いろいろなと不都合な場合があるかもしれません。
そんな時は、例えばアルファベット一文字を使い、「ベクトル \(u\)」というように名前をつけることがおこなわれます。そのような時は、ベクトルであることを強調するために、上に矢印をつけて \(\overrightarrow{u}\)とあらわしたり、太文字にして \(\boldsymbol{u}\) とあらわしたりします。

上の図の場合、\(\overrightarrow{\mathrm{A}\mathrm{B}}\) と \(\overrightarrow{\mathrm{C}\mathrm{D}}\) はどちらも \(\boldsymbol{u}\) という同じ記号であらわすことができます。

ここで説明しているような、平面や空間の矢印として扱うベクトルは幾何ベクトルと呼ばれることがあります。

補足：実は、数学では矢印とは違うやり方で様々なベクトルを考えることができます。

幾何ベクトルの空間

平面や空間の矢印で扱うことのできるベクトルの集合、つまり幾何ベクトルが集まってできる集合のことを考えることにしましょう。 ここではこの集合を、幾何ベクトルの空間と呼ぶことにします。

補足：「空間のベクトル」というときと「幾何ベクトルの空間」というときでは「空間」ということばの意味が違うことに注意しましょう。 前者は私たちが知っている直感的な意味での「空間」で、後者は「集合」という言葉の代わりに使われています。

以後、平面のベクトルをすべて集めてできる幾何ベクトルの空間を \(V^2\) 、空間のベクトルをすべて集めてできる幾何ベクトルの空間を \(V^3\) と書くことにします。
これから説明するように、これらの空間には2つの演算を定義することができます。

幾何ベクトルの空間に定義できる二つの演算

実は、（よく知られているように）\(V^2\) や \(V^3\) には「加法」と「スカラー倍」と呼ばれる演算を定義することができます。ここでは簡単のため、平面のベクトルの場合で考えてみることにします。

\(V^2\) における加法：2つのベクトルの和とは…

ここでは2つのベクトルを「足す」とはどういうことなのかということを定義します。

2つの平面の幾何ベクトル \(\boldsymbol{a}\) と \(\boldsymbol{b}\) があるとします。

これから、これら2つののベクトルの和と呼ばれ、\(\boldsymbol{ a } + \boldsymbol{ b }\) という記号であらわされることになるベクトルを矢印を使って作ることにします。

2通りの作り方を説明します。

作り方その1

まず、平面内の適当なところにベクトル \(\boldsymbol{a}\) をあらわす矢印とベクトル \(\boldsymbol{b}\) をあらわす矢印を描きます。

次にベクトル \(\boldsymbol{a}\) や \(\boldsymbol{b}\) を平行移動して、\(\boldsymbol{b}\) の始点をベクトル \(\boldsymbol{a}\) の終点に合わせます。

そして最後に \(\boldsymbol{a}\) の始点から \(\boldsymbol{b}\) の終点へまっすぐ向かう矢印を描きます。

このようにして描かれた矢印によって代表されるベクトルが \(\boldsymbol{ a } + \boldsymbol{ b }\) です。

次のスライドで確認してみましょう。

作り方その2

まず、平面内の適当なところにベクトル \(\boldsymbol{a}\) をあらわす矢印とベクトル \(\boldsymbol{ b }\) をあらわす矢印を描きます。

次にベクトル \(\boldsymbol{a}\) や \(\boldsymbol{b}\) を平行移動して、\(\boldsymbol{b}\) の始点をベクトル \(\boldsymbol{a}\) の始点に合わせます。

さらに、ベクトル \(\boldsymbol{a}\) と \(\boldsymbol{b}\) が 2つの辺になるように平行四辺形を描きます。

そして最後に \(\boldsymbol{a}\) の始点 （いま、これは \(\boldsymbol{b}\) の始点と一致しています）から 平行四辺形の対角線を矢印で描きます。

このようにして描かれた矢印によって代表されるベクトルが \(\boldsymbol{a} + \boldsymbol{b}\) です。

次のスライドで確認してみましょう。

以上、2つの幾何ベクトルの和の作り方を2通り説明しました。
図を描いて考えればわかりますが、どちらの作り方でも出来上がるベクトルは同じになります。

\(V^2\) におけるスカラー倍：あるベクトルをなんとか倍するとは…

ここでは矢印を伸び縮みさせる操作を定義します。

あるベクトル $ $ とある数 \(r\) があるとします。
ベクトルをあらわす矢印を使って、ベクトル $ $ の \(r\) 倍（詳しくいうとスカラー \(r\) 倍）と呼ばれ、記号 \(r \boldsymbol{a}\) であらわされることになるベクトルを次のようにして作ることにします。

まず、平面内の適当なところにベクトル $ $ をあらわす矢印を描きます。

次に、

\(r>0\) の場合にはこの矢印を向きを変えずに長さを\(r\) 倍した矢印を作り、

\(r<0\) の場合にはこの矢印の向きを逆にして長さを\(|r|\) 倍した矢印を作り、

\(r=0\) のときには長さが \(0\) の矢印を作ります。（長さが \(0\) の矢印は始点と終点が一致する矢印になります。）

このようにしてできる矢印で代表されるベクトルが \(r\boldsymbol{a}\) です。

次のスライドで確認してください。

これまで幾何ベクトルの和とスカラー倍の作り方で説明されてきたようにして、平面のベクトルの集まり \(V^2\) は 「加法」と「スカラー倍」という演算ができる集合となるわけです。

零ベクトルと逆ベクトル

長さが \(0\) の矢印（つまり始点と終点が一致している矢印）であらわされるベクトルを零ベクトルといい、\(\boldsymbol{0}\) であらわします。

あるベクトル \(\boldsymbol{a}\) があるとします。そして、そのベクトルをあらわす矢印の長さは変えずに向きだけを逆にした矢印を作ることを想像してみてください。

この矢印であらわされるベクトルを \(\boldsymbol{a}\) の逆ベクトル といい、\(-\boldsymbol{a}\) であらわします。
これは \(\boldsymbol{a}\) を \(-1\) 倍してできるベクトル \(-1\boldsymbol{a}\) と同じものとなります。

補足：これまでの説明では、ベクトルの空間に直接的には、\(\boldsymbol{a}-\boldsymbol{b}\) というような「減法」は定義されていません。
しかし、加法とスカラー倍を使って \(\boldsymbol{a} + (-\boldsymbol{b})\) というものを作れるようになっているので、これを \(\boldsymbol{a}-\boldsymbol{b}\) と思うことにすれば、 「減法」を扱えるようになるわけです。

加法とスカラー倍が持つ性質

実は加法について以下の法則が成り立ちます。

\[ \begin{align} &\boldsymbol{a} + \boldsymbol{b} = \boldsymbol{b}+\boldsymbol{a} \\ &(\boldsymbol{a} + \boldsymbol{b} ) + \boldsymbol{c} = \boldsymbol{a}+(\boldsymbol{b} + \boldsymbol{c})\\ &\boldsymbol{a} + \boldsymbol{0} = \boldsymbol{a}\\ &\boldsymbol{a} + (-\boldsymbol{a}) = \boldsymbol{0}\\ \end{align} \]

またスカラー倍については以下の法則が成り立ちます。
\[ \begin{align} &r(\boldsymbol{a} + \boldsymbol{b}) = r\boldsymbol{a} + r\boldsymbol{b}\\ &(r+s)\boldsymbol{a} = r \boldsymbol{a} + s \boldsymbol{a}\\ &(rs)\boldsymbol{a} = r(s\boldsymbol{a})\\ &1\boldsymbol{a} = \boldsymbol{a}\\ \end{align} \]

これらの法則は、図を描くことにより簡単に確かめることができます。

たとえば、これらのうちから

\[ (\boldsymbol{a}+\boldsymbol{b}) + \boldsymbol{c} = \boldsymbol{a}+(\boldsymbol{b} + \boldsymbol{c}) \]
という法則がほんとうに成り立っているか確かめてみることにしましょう。

これは、

「さきに \(\boldsymbol{a}\) と \(\boldsymbol{b}\) の和を作ってから次にそれと \(\boldsymbol{c}\) との和を作ったもの」

と、

「さきに \(\boldsymbol{b}\) と \(\boldsymbol{c}\) の和を作ってから次に \(\boldsymbol{a}\) とそれの和を作ったもの」

が等しくなると主張する法則です。 この主張が正しいことは以下の2つのスライドを見れば納得できるでしょう。

ほかの法則についても同じように空間の中にある矢印を想像して考えてみれば、空間のベクトルの集合 \(V^3\) の場合でも以上述べてきたことがすべて成り立つということがわかります。

幾何ベクトルと数ベクトル

ここでは、「矢印であらわされる幾何ベクトルをいくつかの数の組で取り扱う方法」を考えます。

座標系の導入と数ベクトル

幾何ベクトル（平面や空間の矢印であらわされるベクトル）は「どっちに、どれだけ移動するのかということをあらわす矢印」と考えることができます。

ですから、平面や空間になにかしら1つ「（必ずしも直交していなくて構わない）座標系」を描いておけば、平面のベクトルは2つの数の組であらわすことができ、空間のベクトルは3つの数の組であらわすことができます。

次の図の平面ベクトル \(\boldsymbol{a}\) は \(x\) 方向に \(2\)、\(y\) 方 向 に \(-3\) 移動することをあらわす矢印です。 ですから

\[ \boldsymbol{a} = \left( \begin{array}{r} 2\\ -3 \end{array} \right) \]

のように二つの数を縦に並べ組にしてあらわすことができます。

また、次の図の空間ベクトル \(\boldsymbol{a}\) は \(x\) 方向に \(3\)、\(y\) 方向に \(2\) 、\(z\) 方向に \(2\) 移動することをあらわす矢印ですから

\[ \boldsymbol{a} = \left( \begin{array}{r} 3\\ 2\\ 2 \end{array} \right) \] のように三つの数を縦に並べ組にしてあらわすことができます。

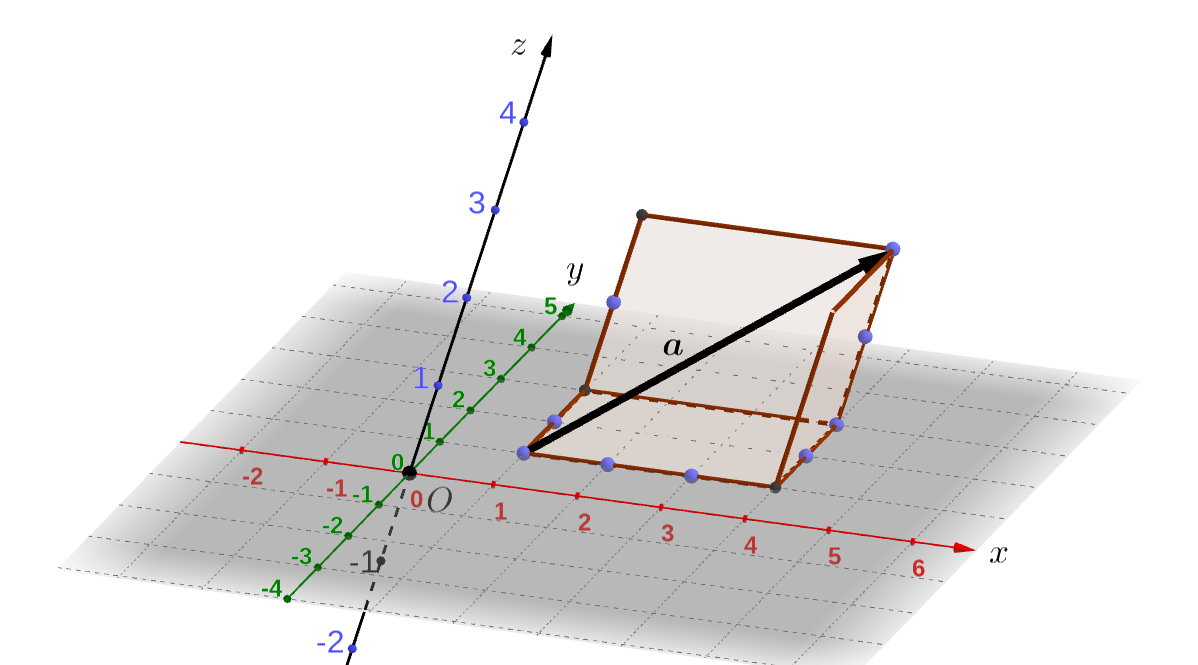
以上のようにして平面ベクトルや空間ベクトルを数の組であらわすことができるわけです。そして、数の組によってあらわされているベクトルは数ベクトルと呼ばれることがあります。

ところで、空間のあるベクトル \(\boldsymbol{a}\) を矢印で代表させて描いたとき、始点の座標が \((x_1, y_1, z_1)\) 、終点の座標が \((x_2, y_2, z_2)\) となっているとしましょう。

この矢印は \(x\) 方向に \(x_2-x_1\)、\(y\) 方 向 に \(y_2-y_1\) 、\(z\) 方向に \(z_2-z_1\) 移動することをあらわしますから、数ベクトルとしてあらわすと、

\[ \boldsymbol{a} = \left( \begin{array}{r} x_2-x_1\\ y_2-y_1\\ z_2-z_1 \end{array} \right) \]

となることがわかります。

特にベクトル \(\boldsymbol{a}\) をあらわす矢印の始点を原点 \(\mathrm{O}\) にしておいた場合は始点の座標が \((0, 0, 0)\) になりますから、終点の座標そのものを縦に並べさえすれば \(\boldsymbol{a}\) を数ベクトルとしてあらわしたことになります。

幾何ベクトル（矢印としてあらわされるベクトル）を数ベクトル（数の組であらわされるベクトル）として扱うとき、「ベクトルを成分であらわす」といったりします。 そして縦に並べられた数は上から順に \(x\) 成分、\(y\) 成分、\(z\) 成分と呼ばれます。

以上の話は、空間のなかのどこかに、1つなにかしらの座標系を固定した上でできる話です。

ところで、空間のなかに座標系を設定する仕方はいくらでもあります。

たとえば、もとの座標系を原点を中心にしてある角度回転させて新しい座標系を設定するとか、\(x\) 軸 と \(y\) 軸を入れ替えて新しい座標系を設定するとか、\(x\) 軸 と \(y\) 軸のなす角を \(60\) 度にして斜めに交わる座標系を設定するとか…無数の座標系を考えることができます。 そして、座標系を変えれば、同じベクトルでも、成分表示は変わってしまうことに注意しましょう。

位置ベクトル

矢印で扱うことのできる幾何ベクトルは「どっちに、どれだけ移動するのか」ということをあらわしますが、次のように考えることにより、「点の位置をあらわす」ために使うことができます。

平面または空間の中に気にしている点 \(\mathrm{P}\) があるとしましょう。

まず、平面または空間のどこかに基準となる点を決め、いつものように原点と呼ぶことにして、\(\mathrm{O}\) という記号であらわしておきます。

つぎに、原点 \(\mathrm{O}\) から、\(\mathrm{P}\) へ向かって矢印を描きます。

始点を原点とすることにしておけば、矢印の終点は気にしている点 \(\mathrm{P}\) そのものです。

ですから、\(\mathrm{O}\) から見た \(\mathrm{P}\) の位置をあらわすために、原点 \(\mathrm{O}\) から出る矢印を使うことができるわけです。

たとえば上の図では、誰かに点 \(\mathrm{P}\) の位置を教えるのためには、「\(\mathrm{P}\) は \(\mathrm{O}\) を基準にして (矢印) \(\boldsymbol{a}\) に従って移動した位置ですよ」と言えば良いわけです。

つまり「この矢印そのものを \(\mathrm{P}\) の位置をあらわすベクトルと考えることができる」わけです。 このように考え、点の位置をあらわすために使うベクトルを位置ベクトルといいます。

たとえば空間で考える場合、原点を通る\(x\) 軸、\(y\) 軸、\(z\) 軸を描いて座標を使うことにすれば、「\(\mathrm{P}\) の座標そのもの」が「\(\mathrm{P}\) の位置ベクトルを成分であらわしたもの」になるのは明らかでしょう。

単位ベクトルと基本ベクトル

どっちの方向を向いているのかに関係なく、とにかく長さが \(1\) のベクトルはどれも単位ベクトル といいます。

空間に普通の直交する座標系（これは正規直交座標系と呼ばれることがあります）が描いてある場合は、次の3つの単位ベクトルがとても役に立ちます。

\[ \boldsymbol{e_1} = \left( \begin{array}{r} 1\\ 0\\ 0 \end{array} \right),\quad \boldsymbol{e_2} = \left( \begin{array}{r} 0\\ 1\\ 0 \end{array} \right),\quad \boldsymbol{e_3} = \left( \begin{array}{r} 0\\ 0\\ 1 \end{array} \right) \]

これらの単位ベクトルはそれぞれ \(x\) 軸、\(y\) 軸、\(z\) 軸に平行で、どれもそれぞれの軸のプラスの方向へ \(1\) 進む矢印であらわされます。

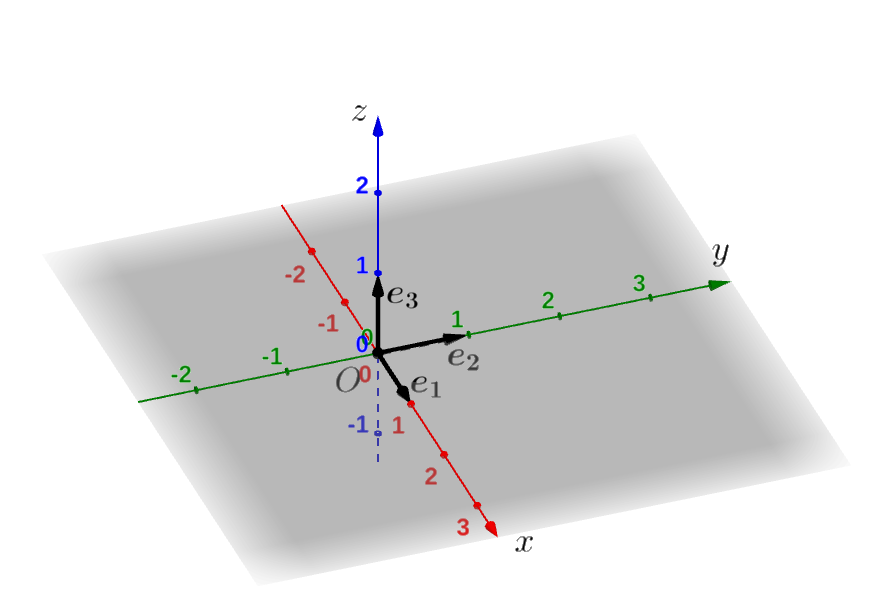
この 3つのベクトルは、\(V^3\)の「この正規直交座標系に関する」基本ベクトルと呼ばれます。

補足：平面のベクトルの場合は、以上の説明で \(z\) 軸 、ベクトルの \(z\) 成分、\(\boldsymbol{e_3}\) などを無視して考えればよいわけです。

補足：ここでは高校で使う教科書に従い基本ベクトルという言葉を使いましたが、大学で使われるような教科書では \(n\) 項単位ベクトルと呼ばれることが多いようです。

まとめ

平面や空間の矢印を「平行移動したときにぴったりと重なるときは同じものだと思う」ことしてそのようなものを幾何ベクトルと呼びます。

幾何ベクトルは足したりスカラー倍することができ、その2つの演算に関してこのページで説明したいくつかの法則が成り立ちます。

座標系を設けると幾何ベクトルを数ベクトルに対応させることができます。

原点を決めておき、原点から出発する矢印を使うと点の位置を矢印で示すことができます。そして点の位置を示す目的で使われる幾何ベクトルを位置ベクトルといいます。

長さが \(1\) のベクトルを単位ベクトルといいます。 平面や空間に正規直交座標系が描いてある場合は、それぞれの軸に沿ってプラスの向きに \(1\) 目盛り進むベクトルが役に立ちます。 これらは基本ベクトル（\(n\) 項単位ベクトル）と呼ばれます。