計量線形空間の基底とその変換
2023-05-14
グラム・シュミットの直交化と正規直交基底
１つの線形空間には基底が無数に存在しますが、内積が定義されている線形空間（つまり計量線形空間）の基底としてふさわしいのはどんなものでしょうか。
内積の計算と相性が良い基底は、互いに直交するベクトルから作られているものであると考えられます。ところで、そのような基底は存在するのでしょうか？
実は、計量線形空間（内積の定義されている線形空間）では、その内積を使いある手順を踏むことにより、任意の基底から直交するベクトルだけからなる基底を得ることができます。このことをこれから説明することにします。
グラム・シュミットの直交化
\(V\) を \(\mathbb{K}\) 上の計量線形空間とし、\(V\) のベクトル \(\boldsymbol{x}\) と \(\boldsymbol{y}\) の内積を \((\boldsymbol{x},\boldsymbol{y})\) であらわすことにします。また、\(\boldsymbol{a}_1,\boldsymbol{a}_2,\ldots,\boldsymbol{a}_k\) を \(V\) の \(k\) 個の一次独立なベクトルとします。このとき、\(V\) の \(k\) 個のベクトル \(\boldsymbol{u}_1,\boldsymbol{u}_2,\ldots,\boldsymbol{u}_k\) を、以下の条件を満たすようにつくることができます。
- \(\boldsymbol{u}_1,\boldsymbol{u}_2,\ldots,\boldsymbol{u}_k\) はどれも \(\boldsymbol{a}_1,\boldsymbol{a}_2,\ldots,\boldsymbol{a}_k\) の一次結合となっている。
- \(\boldsymbol{u}_1,\boldsymbol{u}_2,\ldots,\boldsymbol{u}_k\) は互いに直交する。
- \(\boldsymbol{u}_1,\boldsymbol{u}_2,\ldots,\boldsymbol{u}_k\) の長さはどれも \(1\) である。
それでは、このような \(\boldsymbol{u}_1,\boldsymbol{u}_2,\ldots,\boldsymbol{u}_k\) をつくる手順をこれから説明します。
空間の幾何ベクトルの場合でアイデアを説明しておくと…
幾何ベクトルの正射影
これは、ベクトル \(\boldsymbol{b}\) に垂直な方向からベクトル \(\boldsymbol{a}\) に光をあてたところ、ベクトル \(\boldsymbol{b}\) の上に影として緑色のベクトルができたところをあらわしています。
この図のベクトル \(\boldsymbol{u}\) はベクトル \(\boldsymbol{b}\) と方向が同じで長さが \(1\) のベクトルです。
また、 また、\(\theta\) は \(\boldsymbol{a}\) と \(\boldsymbol{u}\) のなす角をあらわしています。
ところで、幾何ベクトルの自然内積 \((\,\,\,,\,\,)\) では、\[ \begin{align} (\boldsymbol{a}, \boldsymbol{u}) &= \|\boldsymbol{a}\|\|\boldsymbol{u}\|\cos\theta\\ &= \|\boldsymbol{a}\| \cos \theta\\ \end{align} \]
が成り立っています。
またここで、（たとえば高校で学んだ） \(\cos\theta\) のそもそもの定義を思い出してみれば、\(\theta\) が \(0\) 以上 \(\frac{\pi}{2}\) 以下のとき、\(\|\boldsymbol{a}\|\cos\theta\) は緑色のベクトルの長さに等しく、
\(\theta\) が \(\frac{\pi}{2}\) 以上 \(\pi\) 以下のとき、\(\|\boldsymbol{a}\|\cos\theta\) は緑色のベクトルの長さに\(-1\) を掛けたものに等しい
ということがわかります。
というわけで、ベクトル向きのことまでちゃんと考えると、\(\theta\) が \(0\) 以上 \(\frac{\pi}{2}\) 以下の場合、\(\theta\) が \(\frac{\pi}{2}\) 以上 \(\pi\) 以下の場合のどちらにおいても、緑色のベクトルは、\((\boldsymbol{a}, \boldsymbol{u})\boldsymbol{u}\) とあらわされる
ということになります。このようにして得られる（図では緑色の）ベクトルを \(\boldsymbol{a}\) の \(\boldsymbol{u}\) 方向への正射影といいます。
正射影を利用して垂直なベクトルを得る
\[ \boldsymbol{v}'=\boldsymbol{a}-(\boldsymbol{a}, \boldsymbol{u})\boldsymbol{u} \]
として作られるベクトル \(\boldsymbol{v}'\) はベクトル \(\boldsymbol{u}\) に垂直になります。そしてさらに、\(\boldsymbol{v}'\) をその長さで割ったベクトル \(\boldsymbol{v}\) を作れば、\(\boldsymbol{u}\) に垂直で長さが \(1\) のベクトルとなるわけです。
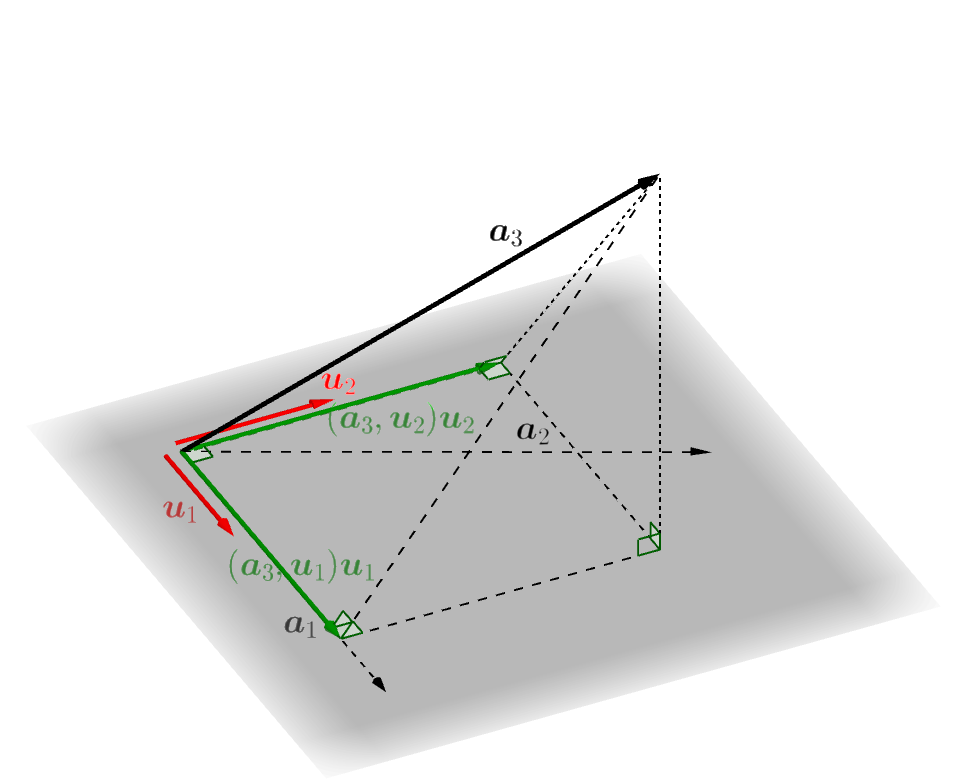
空間の幾何ベクトルの世界で一次独立な3つのベクトルから長さが \(1\) で互いに垂直な３つのベクトルを得る手順
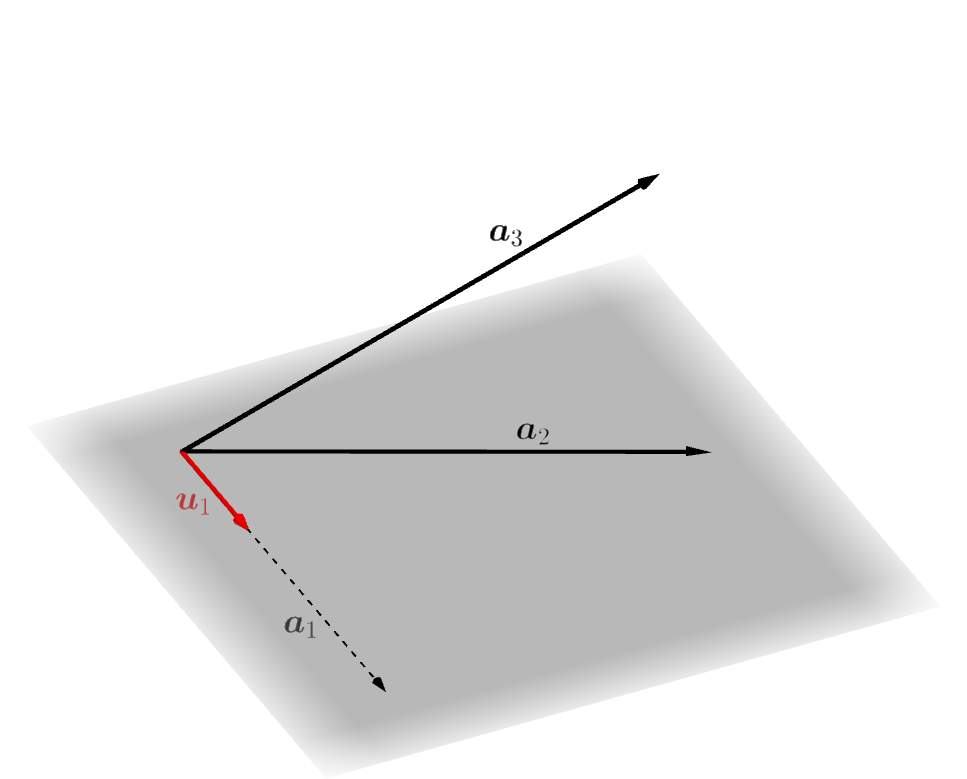
次のスライドを見てください。空間の幾何ベクトルの世界で３つの一次独立なベクトル \(\boldsymbol{a}_1,\boldsymbol{a}_2,\boldsymbol{a}_3\) から、互いに垂直で長さが \(1\) である３つのベクトル \(\boldsymbol{u}_1,\boldsymbol{u}_2,\boldsymbol{u}_3\) を作る手順が説明されています。空間の中に３つの一次独立なベクトル \(\boldsymbol{a}_1,\boldsymbol{a}_2,\boldsymbol{a}_3\) があります。
\(\boldsymbol{u}_1=\frac{\boldsymbol{a}_1}{\|\boldsymbol{a}_1\|}\) を作ると \(\boldsymbol{a}_1\) と同じ方向で長さが \(1\) のベクトルが得られます。
\(\boldsymbol{a}_2\) の \(\boldsymbol{u}_1\) 方向への正射影 \((\boldsymbol{a}_1,\boldsymbol{u}_1)\boldsymbol{u}_1\) を作ります。
\(\boldsymbol{u}'_2= \boldsymbol{a}_2-(\boldsymbol{a}_1,\boldsymbol{u}_1)\boldsymbol{u}_1\) を作るとこれは \(\boldsymbol{u}_1\) に垂直になります。
\(\boldsymbol{u}'_2\) を平行移動し、その長さで割って \(\boldsymbol{u}_2=\frac{\boldsymbol{u}'_2}{\|\boldsymbol{u}'_2\|}\) を作るとこれは長さが \(1\) で \(\boldsymbol{u}_1\) に垂直になります。
\(\boldsymbol{a}_3\) の \(\boldsymbol{u}_1\) 方向への正射影 \((\boldsymbol{a}_3,\boldsymbol{u}_1)\boldsymbol{u}_1\) と \(\boldsymbol{u}_2\) 方向への正射影 \((\boldsymbol{a}_3,\boldsymbol{u}_2)\boldsymbol{u}_2\) を作ります。
\((\boldsymbol{a}_3,\boldsymbol{u}_1)\boldsymbol{u}_1 +(\boldsymbol{a}_3,\boldsymbol{u}_2)\boldsymbol{u}_2\) は \(\boldsymbol{a}_3\) の灰色の平面への正射影になっています。
\(\boldsymbol{u}'_3= \boldsymbol{a}_3-(\boldsymbol{a}_3,\boldsymbol{u}_1)\boldsymbol{u}_1-(\boldsymbol{a}_3,\boldsymbol{u}_2)\boldsymbol{u}_2\) を作るとこれは \(\boldsymbol{u}_1,\boldsymbol{u}_2\) に垂直になります。
\(\boldsymbol{u}'_3\) を平行移動し、その長さで割って \(\boldsymbol{u}_3=\frac{\boldsymbol{u}'_3}{\|\boldsymbol{u}'_3\|}\) を作るとこれは長さが \(1\) で \(\boldsymbol{u}_1,\boldsymbol{u}_2\) に垂直になります。
一般の計量線形空間の場合
空間の幾何ベクトルの場合の手順と同じようにして、一般の計量線形空間の場合でも互いに直交し長さが \(1\) のベクトルを作っていくことができます。図を描いたり矢印を使うわけには行きませんが、以下にその手順を説明します。
１つ目のベクトル \(\boldsymbol{u}_1\) を作ります。 \(\boldsymbol{a}_1,\boldsymbol{a}_2,\ldots,\boldsymbol{a}_k\) は一次独立なベクトル なのでもちろん \(\boldsymbol{a}_1\) は零ベクトルではありません。ですから \(\|\boldsymbol{a}_1\|\) は \(0\) ではありません。そこで、\[\boldsymbol{u}_1=\frac{\boldsymbol{a}_1}{\|\boldsymbol{a}_1\|} \tag{1}\]
とすることにより、長さ \(1\) のベクトル \(\boldsymbol{u}_1\) をつくることができます。このとき、\(\boldsymbol{u}_1\) は \(\boldsymbol{a}_1\) の一次結合（この場合は特にスカラー倍）となっていますから、
\(\boldsymbol{u}_1\) の一次結合としてあらわされるベクトルは \(\boldsymbol{a}_1\) の一次結合としてあらわすことができ、その逆も成り立つ
\[\boldsymbol{u}_1 \text{の張る} V \text{の部分空間} = \boldsymbol{a}_1 \text{の張る} V \text{の部分空間} \tag{1'}\]
ということが成り立ちます。
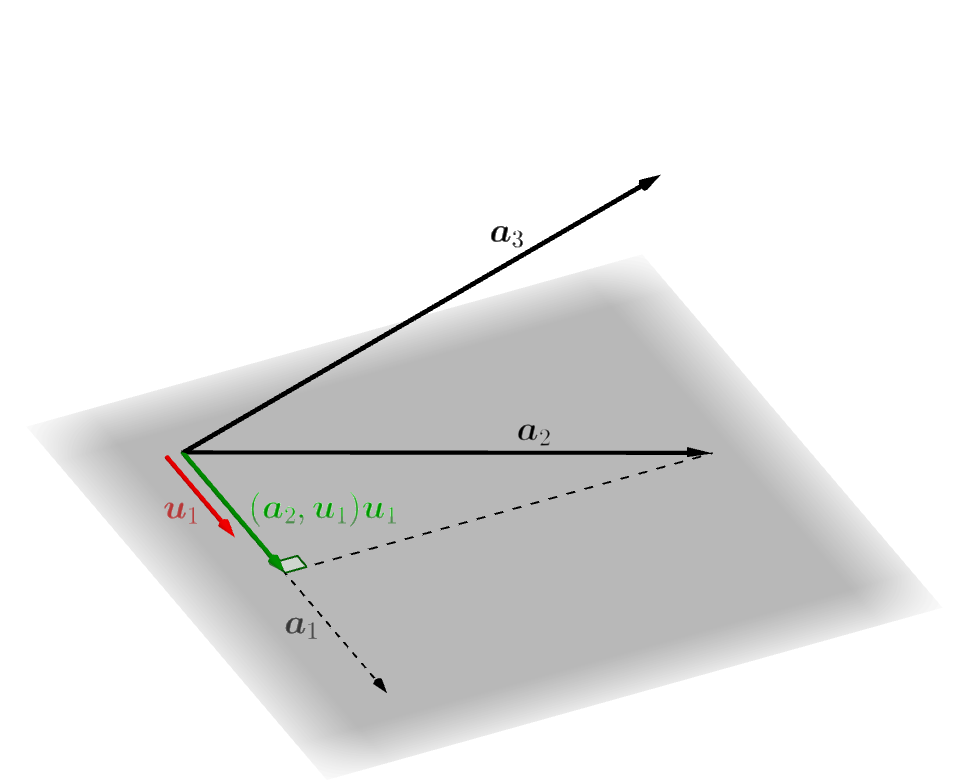
２つ目のベクトル \(\boldsymbol{u}_2\) を作ります。まず、\[ \boldsymbol{u}'_2 = \boldsymbol{a}_2-(\boldsymbol{a}_2,\boldsymbol{u}_1)\boldsymbol{u}_1 \tag{2} \]
\[ \begin{align} (\boldsymbol{u}'_2,\boldsymbol{u}_1) &=(\boldsymbol{a}_2-(\boldsymbol{a}_2,\boldsymbol{u}_1)\boldsymbol{u}_1,\boldsymbol{u}_1)\\ &=(\boldsymbol{a}_2,\boldsymbol{u}_1)-(\boldsymbol{a}_2,\boldsymbol{u}_2)\|\boldsymbol{u}_1\|\\ &=0 \end{align} \]
が成り立ち内積の値が \(0\) になります。また、\(\boldsymbol{u}'_2\) は零ベクトルではないことが次のようにしてわかります。 もし、 \(\boldsymbol{u}'_2 = \boldsymbol{0}\) とすると、\((2)\) 式より、\(\boldsymbol{a}_2=(\boldsymbol{a}_2,\boldsymbol{u}_1)\boldsymbol{u}_1\) となり \(\boldsymbol{a}_2\) は \(\boldsymbol{u}_1\) の一次結合となります。ところで、\((1')\) 式（またはその前に書かれていたこと）を思い出すと、さらに、\(\boldsymbol{a}_2\) は \(\boldsymbol{a}_1\) の一次結合であることになってしまいますが、これは \(\boldsymbol{a}_1,\boldsymbol{a}_2\) が一次独立であることに矛盾します。
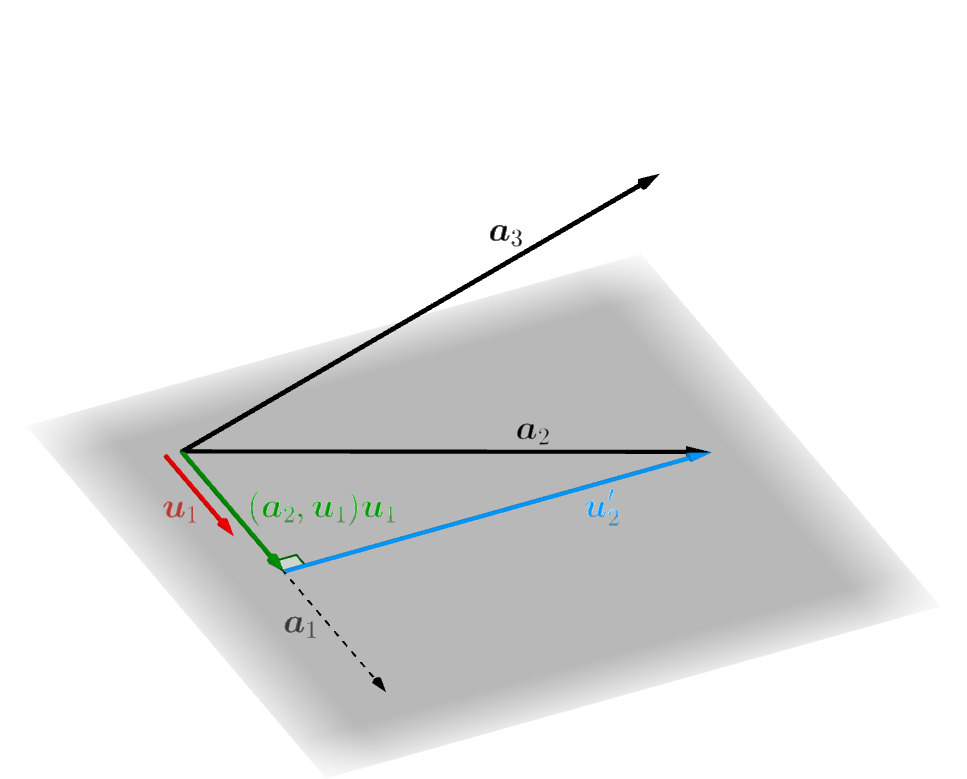
というわけで、\[ \boldsymbol{u}_2=\frac{\boldsymbol{u}'_2}{\|\boldsymbol{u}'_2\|} \]
とすれば、これは \(\boldsymbol{u}_1\) と直交するだけではなく、長さが \(1\) のベクトルになります。
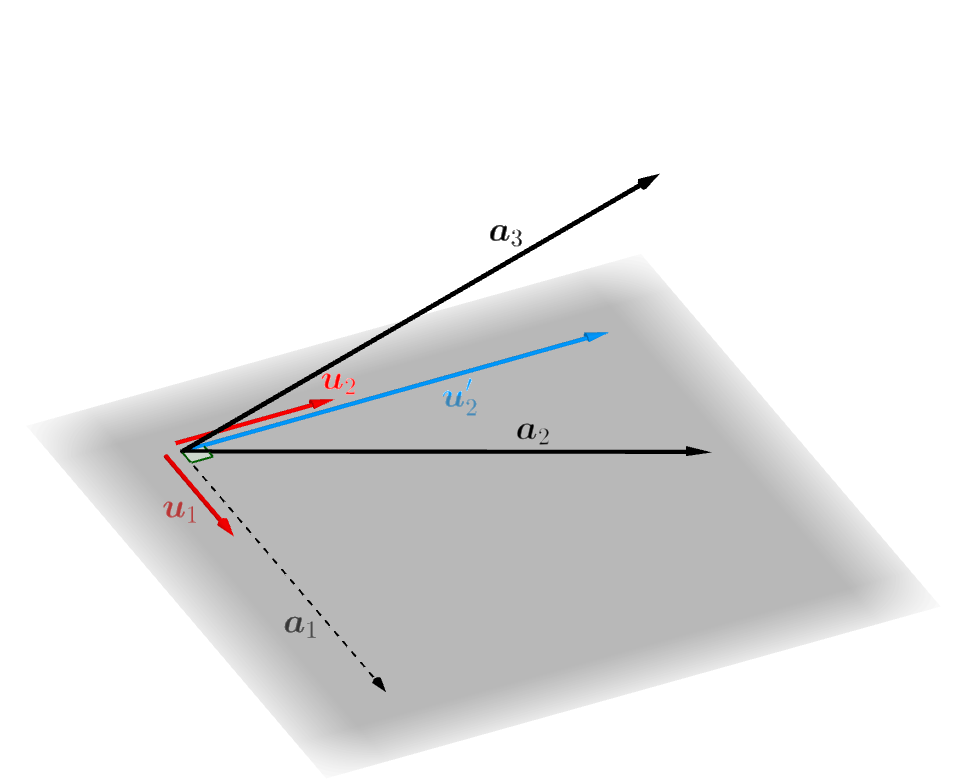
このとき、\((2)\) 式と、\(\boldsymbol{u}_2\) が \(\boldsymbol{u}'_2\) のスカラー倍であることに注意すると、\(\boldsymbol{u}_2\) は \(\boldsymbol{u}_1,\boldsymbol{a}_2\) の一次結合としてあらわされ、\(\boldsymbol{a}_2\) は \(\boldsymbol{u}_1,\boldsymbol{u}_2\) の一次結合としてあらわされることがわかります。ですから、
\(\boldsymbol{u}_1,\boldsymbol{u}_2\) の一次結合としてあらわされるベクトルは \(\boldsymbol{a}_1,\boldsymbol{a}_2\) の一次結合としてあらわすことができ、その逆も成り立つ
\[\boldsymbol{u}_1,\boldsymbol{u}_2 \text{の張る} V \text{の部分空間} = \boldsymbol{a}_1,\boldsymbol{a}_2 \text{の張る} V \text{の部分空間} \tag{2'} \]
ということが成り立ちます。
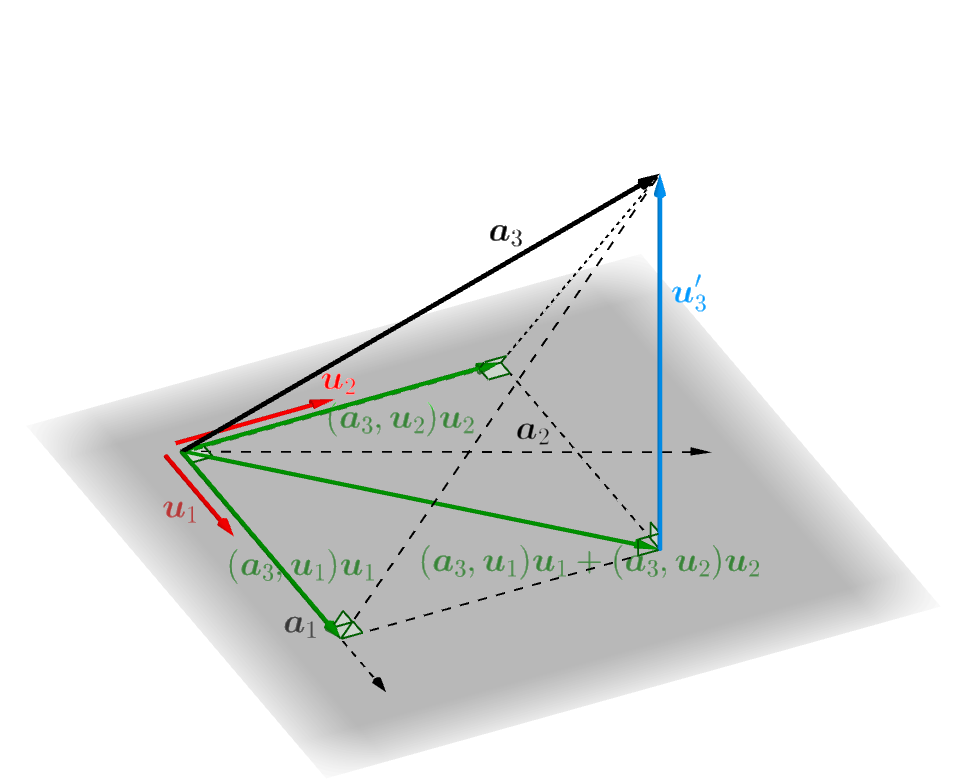
３つ目のベクトル \(\boldsymbol{u}_3\) を作ります。まず、\[ \boldsymbol{u}'_3 = \boldsymbol{a}_3-(\boldsymbol{a}_3,\boldsymbol{u}_1)\boldsymbol{u}_1-(\boldsymbol{a}_3,\boldsymbol{u}_2)\boldsymbol{u}_2 \tag{3} \]
として \(\boldsymbol{u}'_3\) をつくると、これは \(\boldsymbol{u}_1,\boldsymbol{u}_2\) と直交します。実際、\(\boldsymbol{u}_1,\boldsymbol{u}_2\) は直交し長さは \(1\) であることとに注意して計算をすると
\[ \begin{align} (\boldsymbol{u}'_3,\boldsymbol{u}_1) &=(\boldsymbol{a}_3-(\boldsymbol{a}_3,\boldsymbol{u}_1)\boldsymbol{u}_1-(\boldsymbol{a}_3,\boldsymbol{u}_2)\boldsymbol{u}_2,\boldsymbol{u}_1)\\ &=(\boldsymbol{a}_3,\boldsymbol{u}_1)-(\boldsymbol{a}_3,\boldsymbol{u}_1)\|\boldsymbol{u}_1\|-(\boldsymbol{a}_3,\boldsymbol{u}_2)(\boldsymbol{u}_2,\boldsymbol{u}_1)\\ &=(\boldsymbol{a}_3,\boldsymbol{u}_1)-(\boldsymbol{a}_3,\boldsymbol{u}_1)\\ &=0\\ (\boldsymbol{u}'_3,\boldsymbol{u}_2) &=(\boldsymbol{a}_3-(\boldsymbol{a}_3,\boldsymbol{u}_2)\boldsymbol{u}_1-(\boldsymbol{a}_3,\boldsymbol{u}_2)\boldsymbol{u}_2,\boldsymbol{u}_2)\\ &=(\boldsymbol{a}_3,\boldsymbol{u}_2)-(\boldsymbol{a}_3,\boldsymbol{u}_2)(\boldsymbol{u}_1,\boldsymbol{u}_2)-(\boldsymbol{a}_3,\boldsymbol{u}_2)\|\boldsymbol{u}_2\|\\ &=(\boldsymbol{a}_3,\boldsymbol{u}_2)-(\boldsymbol{a}_3,\boldsymbol{u}_2)\\ &=0\\ \end{align} \]
となり内積の値が \(0\) になります。
また、\(\boldsymbol{u}'_3\) は零ベクトルではないことが次のようにしてわかります。 もし、 \(\boldsymbol{u}'_3 = \boldsymbol{0}\) とすると、\((3)\) 式より、\(\boldsymbol{a}_3=(\boldsymbol{a}_3,\boldsymbol{u}_1)\boldsymbol{u}_1 + (\boldsymbol{a}_3,\boldsymbol{u}_2)\boldsymbol{u}_2\) となり \(\boldsymbol{a}_3\) は \(\boldsymbol{u}_1,\boldsymbol{u}_2\) の一次結合となります。ところで、\((2')\) 式（またはその前に書かれていたこと）を思い出すと、さらに、\(\boldsymbol{a}_3\) は \(\boldsymbol{a}_1,\boldsymbol{a}_2\) の一次結合であることになってしまいますが、これは \(\boldsymbol{a}_1,\boldsymbol{a}_2,\boldsymbol{a}_3\) が一次独立であることに矛盾します。
というわけで、
\[ \boldsymbol{u}_3=\frac{\boldsymbol{u}'_3}{\|\boldsymbol{u}'_3\|} \]
とすれば、これは \(\boldsymbol{u}_1,\boldsymbol{u}_2\) と直交するだけではなく、長さが \(1\) のベクトルになります。
このとき、\((3)\) 式と、\(\boldsymbol{u}_3\) が \(\boldsymbol{u}'_3\) のスカラー倍であることに注意すると、\(\boldsymbol{u}_3\) は \(\boldsymbol{u}_1,\boldsymbol{u}_2,\boldsymbol{a}_3\) の一次結合としてあらわされ、\(\boldsymbol{a}_3\) は \(\boldsymbol{u}_1,\boldsymbol{u}_2,\boldsymbol{u}_3\) の一次結合としてあらわされることがわかります。ですから、
\(\boldsymbol{u}_1,\boldsymbol{u}_2,\boldsymbol{u}_3\) の一次結合としてあらわされるベクトルは \(\boldsymbol{a}_1,\boldsymbol{a}_2,\boldsymbol{a}_3\) の一次結合としてあらわすことができ、その逆も成り立つ
\[\boldsymbol{u}_1,\boldsymbol{u}_2,\boldsymbol{u}_3 \text{の張る} V \text{の部分空間} = \boldsymbol{a}_1,\boldsymbol{a}_2,\boldsymbol{a}_3 \text{の張る} V \text{の部分空間} \tag{3'} \]
ということが成り立ちます。
以上のような方法は、最後のベクトルをつくるまで繰り返すことができます。
\(k\) 個目のベクトルを作ります。\[ \boldsymbol{u}'_k = \boldsymbol{a}_k-(\boldsymbol{a}_3,\boldsymbol{u}_1)\boldsymbol{u}_1-(\boldsymbol{a}_3,\boldsymbol{u}_2)\boldsymbol{u}_2-\cdots-(\boldsymbol{a}_k,\boldsymbol{u}_{k-1})\boldsymbol{u}_{k-1} \]
として \(\boldsymbol{u}'_k\) をつくると、これは \(\boldsymbol{u}_1,\boldsymbol{u}_2,\ldots,\boldsymbol{u}_{k-1}\) と直交することをこれまでと同様の計算で確認できます。そして零ベクトルではないこともこれまでと同様に確認できます。
そこで、\[ \boldsymbol{u}_k=\frac{\boldsymbol{u}'_k}{\|\boldsymbol{u}'_k\|} \]
とすれば、これは \(\boldsymbol{u}_1,\boldsymbol{u}_2,\ldots,\boldsymbol{u}_{k-1}\) と直交するだけではなく、長さが \(1\) です。
以上で 条件を満たす \(\boldsymbol{u}_1,\ldots,\boldsymbol{u}_k\) をつくることができました。
ここで説明した方法はグラム・シュミットの直交化と呼ばれています。
補足
ここで説明したグラム・シュミットの直交化の方法を振り返ると、
\(\boldsymbol{a}_1\) で生成される部分空間 \(=\boldsymbol{u}_1\) で生成される部分空間
\(\boldsymbol{a}_1,\boldsymbol{a}_2\) で生成される部分空間 \(=\boldsymbol{u}_1,\boldsymbol{u}_2\) で生成される部分空間
\(\boldsymbol{a}_1,\boldsymbol{a}_2,\boldsymbol{a}_3\) で生成される部分空間 \(=\boldsymbol{u}_1,\boldsymbol{u}_2,\boldsymbol{u}_3\) で生成される部分空間
︙
\(\boldsymbol{a}_1,\boldsymbol{a}_2,\boldsymbol{a}_3,\cdots,\boldsymbol{a}_k\) で生成される部分空間 \(=\boldsymbol{u}_1,\boldsymbol{u}_2,\boldsymbol{u}_3,\cdots,\boldsymbol{u}_k\) で生成される部分空間
となっていることがわかります。
正規直交基底
\(\mathbb{K}\) 上の \(n\) 次元計量線形空間 \(V\) の基底 \(\lt \boldsymbol{u}_1,\boldsymbol{u}_2,\ldots,\boldsymbol{u}_n \gt\) が内積に関して、\[ (\boldsymbol{u}_i,\boldsymbol{u}_j) =\begin{cases}1 & (i=j)\\ 0 & (i \neq j) \end{cases} \]
を満たしているとき、\(\lt \boldsymbol{u}_1,\boldsymbol{u}_2,\ldots,\boldsymbol{u}_n \gt\) は正規直交基底と呼ばれます。 つまり、基底の各ベクトルの長さは \(1\) で、異なるベクトルは互いに直交しているとき、その基底を正規直交基底と呼ぶわけです。
正規直交基底は計量線形空間のベクトルについて様々な計算をおこなうとき、最も役に立つ基底と考えられますが、どんな計量線形空間にも正規直交基底は存在するのでしょうか？ その問いに答えるのが次の定理です。
定理
\(\mathbb{K}\) 上の有限次元計量線形空間には正規直交基底が存在します。
証明
\(n\) 次元の計量線形空間には、とにかく、（必ずしも正規直交とは限らない）基底 \(\lt \boldsymbol{a}_1,\boldsymbol{a}_2, \ldots ,\boldsymbol{a}_n \gt\) が存在します。 そして、グラム・シュミットの直交化をおこなうことにより、基底 \(\lt \boldsymbol{a}_1,\boldsymbol{a}_2, \ldots ,\boldsymbol{a}_n \gt\) から正規直交基底 \(\lt \boldsymbol{u}_1,\boldsymbol{u}_2,\ldots,\boldsymbol{u}_n \gt\) をつくることができます。例
\(3\) 次元数ベクトル空間 \(\mathbb{K}^3\) のベクトル\[\boldsymbol{a}_1=\left(\begin{array}{r} 2\\4\\4 \end{array}\right), \boldsymbol{a}_2=\left(\begin{array}{r} 3\\0\\3 \end{array}\right), \boldsymbol{a}_3=\left(\begin{array}{r} 8\\4\\4 \end{array}\right) \]
が一次独立であることはそれなりに頑張ると確認できます。ですから、\(\lt\boldsymbol{a}_1,\boldsymbol{a}_2,\boldsymbol{a}_3\gt\) は基底になります。
これからグラム・シュミットの直交化を使い、\(\mathbb{K}^3\) の自然内積に関する正規直交基底を作ってみることにします。
\(\boldsymbol{u}_1\) を求めます。
\(\|\boldsymbol{a}_1\|=\sqrt{2^2+4^2+4^2}=6\) となるので\[ \begin{align} \boldsymbol{u}_1&=\frac{\boldsymbol{a}_1}{\|\boldsymbol{a}_1\|}=\frac{1}{6}\left(\begin{array}{r} 2\\4\\4 \end{array}\right)=\frac{1}{3}\left(\begin{array}{r} 1\\2\\2 \end{array}\right)\\ \end{align} \]
が得られます。
\(\boldsymbol{u}_2\) を求めます。
\[\displaystyle(\boldsymbol{a}_2,\boldsymbol{u}_1) =\left(\left(\begin{array}{r} 3\\0\\3 \end{array}\right),\frac{1}{3}\left(\begin{array}{r} 1\\2\\2 \end{array}\right)\right) =\frac{1}{3}\left(\left(\begin{array}{r} 3\\0\\3 \end{array}\right),\left(\begin{array}{r} 1\\2\\2 \end{array}\right)\right) =\frac{1}{3}(3\cdot1+0\cdot 2+ 3 \cdot 2)=3\]
となるので
\[ \begin{align} \boldsymbol{u}'_2 &= \boldsymbol{a}_2-(\boldsymbol{a}_2,\boldsymbol{u}_1)\boldsymbol{u}_1\\ &=\left(\begin{array}{r} 3\\0\\3 \end{array}\right)-3\cdot\frac{1}{3}\left(\begin{array}{r} 1\\2\\2 \end{array}\right)\\ &=\left(\begin{array}{r} 2\\-2\\1 \end{array}\right) \end{align} \]
となります。そして \(\|\boldsymbol{u}'_2\|=\sqrt{2^2+(-2)^2+1^2}=3\) となるので
\[ \boldsymbol{u}_2=\frac{\boldsymbol{u}'_2}{\|\boldsymbol{u}'_2\|}=\frac{1}{3}\left(\begin{array}{r} 2\\-2\\1 \end{array}\right) \]
が得られます。
\(\boldsymbol{u}_3\) を求めます。
\[\displaystyle(\boldsymbol{a}_3,\boldsymbol{u}_1) =\left(\left(\begin{array}{r} 8\\4\\4 \end{array}\right),\frac{1}{3}\left(\begin{array}{r} 1\\2\\2 \end{array}\right)\right) =\frac{1}{3}\left(\left(\begin{array}{r} 8\\4\\4 \end{array}\right),\left(\begin{array}{r} 1\\2\\2 \end{array}\right)\right) =\frac{1}{3}(8\cdot1+4\cdot 2+ 4 \cdot 2)=8\]
\[\displaystyle(\boldsymbol{a}_3,\boldsymbol{u}_2) =\left(\left(\begin{array}{r} 8\\4\\4 \end{array}\right),\frac{1}{3}\left(\begin{array}{r} 2\\-2\\1 \end{array}\right)\right) =\frac{1}{3}\left(\left(\begin{array}{r} 8\\4\\4 \end{array}\right),\left(\begin{array}{r} 2\\-2\\1 \end{array}\right)\right) =\frac{1}{3}(8\cdot2+4\cdot(- 2)+ 4 \cdot 1)=4\]
となるので
\[ \begin{align} \boldsymbol{u}'_3 &= \boldsymbol{a}_3-(\boldsymbol{a}_3,\boldsymbol{u}_1)\boldsymbol{u}_1-(\boldsymbol{a}_3,\boldsymbol{u}_2)\boldsymbol{u}_2\\ &=\left(\begin{array}{r} 8\\4\\4 \end{array}\right) -8\cdot\frac{1}{3}\left(\begin{array}{r} 1\\2\\2 \end{array}\right)-4\cdot\frac{1}{3}\left(\begin{array}{r} 2\\-2\\1 \end{array}\right)\\ &=\frac{1}{3}\left(\begin{array}{r} 8\\4\\-8 \end{array}\right)\\ \end{align} \]
となります。そして \(\displaystyle\|\boldsymbol{u}'_3\|=\frac13\sqrt{8^2+4^2+(-8)^2}=4\) となるので
\[ \boldsymbol{u}_3 =\frac{\boldsymbol{u}'_3}{\|\boldsymbol{u}'_3\|}=\frac14\cdot\frac{1}{3}\left(\begin{array}{r} 8\\4\\-8 \end{array}\right)=\frac{1}{3}\left(\begin{array}{r} 2\\1\\-2 \end{array}\right) \]
が得られます。
\[ \left\lt\boldsymbol{u}_1=\frac{1}{3}\left(\begin{array}{r} 1\\2\\2 \end{array}\right), \boldsymbol{u}_2=\frac{1}{3}\left(\begin{array}{r} 2\\-2\\1 \end{array}\right), \boldsymbol{u}_3=\frac{1}{3}\left(\begin{array}{r} 2\\1\\-2 \end{array}\right) \right\gt \]
を作ることができました。
正規直交基底と座標による内積の表示
\(V\) を \(\mathbb{K}\) 上の \(n\) 次元の計量線形空間とし、\(V\) のベクトル \(\boldsymbol{x},\boldsymbol{y}\) の内積を \(\left(\boldsymbol{x},\boldsymbol{y}\right)\) であらわすことにします。 また、\(\lt \boldsymbol{u}_1,\boldsymbol{u}_2,\ldots,\boldsymbol{u}_n \gt\) を \(V\) の正規直交基底とします。
\(\boldsymbol{x},\boldsymbol{y}\) をこの正規直交基底を用いて \[ \begin{align} \boldsymbol{x}&=x_1\boldsymbol{u}_1 + \cdots + x_n\boldsymbol{u}_n \\ \boldsymbol{y}&=y_1\boldsymbol{u}_1 + \cdots + y_n\boldsymbol{u}_n \end{align} \] とあらわすことにして \(\left(\boldsymbol{x},\boldsymbol{y}\right)\) を計算してみることにします。 内積の共役線形性と\(\lt \boldsymbol{u}_1,\boldsymbol{u}_2,\ldots,\boldsymbol{u}_n \gt\) は正規直交していることを用いると \[ \begin{align} \left(\boldsymbol{x},\boldsymbol{y}\right) &=\left(x_1\boldsymbol{u}_1 + \cdots + x_n\boldsymbol{u}_n,y_1\boldsymbol{u}_1 + \cdots + y_n\boldsymbol{u}_n\right)\\ &=x_1\overline{y_1}+x_2\overline{y_2}+\cdots+x_n\overline{y_n} \end{align} \] となることがわかります。 つまり、正規直交基底を用いてベクトルを座標で扱うと、計量線形空間の内積は数ベクトル空間の自然内積と同じ見かけになるわけです。
内積を保つ基底変換
計量線形空間の基底として都合がよいのは正規直交基底ですから、基底変換を考える場合、正規直交基底を正規直交基底へ変換するものが大切であると考えられます。
\(V\) を \(\mathbb{K}\) 上の \(n\) 次元計量線形空間とし、 \(\lt \boldsymbol{u}_1,\boldsymbol{u}_2,\ldots,\boldsymbol{u}_n \gt\) を \(V\) の正規直交基底とし、\(\lt \boldsymbol{b}_1,\boldsymbol{b}_2,\ldots,\boldsymbol{b}_n \gt\) を \(V\) の必ずしも正規直交とは限らない基底とします。 ではここで、\(\lt \boldsymbol{u}_1,\boldsymbol{u}_2,\ldots,\boldsymbol{u}_n \gt\) から \(\lt \boldsymbol{b}_1,\boldsymbol{b}_2,\ldots,\boldsymbol{b}_n \gt\) への基底変換の行列を \(P=\left( \begin{array}{cccc} p_{ 11 } & p_{ 12 } & \ldots & p_{ 1n } \\ p_{ 21 } & p_{ 22 } & \ldots & p_{ 2n } \\ \vdots & \vdots & \ddots & \vdots \\ p_{ n1 } & p_{ n2 } & \ldots & p_{ nn } \end{array} \right)\) とおき、\(\lt \boldsymbol{b}_1,\boldsymbol{b}_2,\ldots,\boldsymbol{b}_n \gt\) が正規直交基底となるためには \(P\) はどんな行列でなくてはならないのか調べてみることにしましょう。
基底変換の行列 \(P\) は\[ \left(\boldsymbol{b}_1,\boldsymbol{b}_2, \ldots,\boldsymbol{b}_n\right)=\left(\boldsymbol{u}_1,\boldsymbol{u}_2,\ldots,\boldsymbol{u}_n \right) \left( \begin{array}{cccc} p_{ 11 } & p_{ 12 } & \ldots & p_{ 1n } \\ p_{ 21 } & p_{ 22 } & \ldots & p_{ 2n } \\ \vdots & \vdots & \ddots & \vdots \\ p_{ n1 } & p_{ n2 } & \ldots & p_{ nn } \end{array} \right) \]
\[ \boldsymbol{b}_k= p_{1k}\boldsymbol{u}_1 + \cdots + p_{nk}\boldsymbol{u}_n \]
\[ \begin{align} (\boldsymbol{b}_i,\boldsymbol{b}_j) &=(p_{1i}\boldsymbol{u}_1 + \cdots + p_{ni}\boldsymbol{u}_n,p_{1j}\boldsymbol{u}_1 + \cdots + p_{nj}\boldsymbol{u}_n)\\ &=p_{1i}\overline{p_{1j}}+p_{2i}\overline{p_{2j}}+\cdots+p_{ni}\overline{p_{nj}}\\ \end{align} \tag{4} \]
となることがわかります。
\(\lt \boldsymbol{b}_1,\boldsymbol{b}_2,\ldots,\boldsymbol{b}_n \gt\) が正規直交基底であるということは、
\[ (\boldsymbol{b}_i,\boldsymbol{b}_j) =\begin{cases}1 & (i=j)\\ 0 & (i \neq j) \end{cases} \]
が成り立つということですから、\((4)\) 式より、このとき基底変換の行列 \(P\) の成分は
\[ p_{1i}\overline{p_{1j}}+p_{2i}\overline{p_{2j}}+\cdots+p_{ni}\overline{p_{nj}}=\begin{cases} 1 & (i=j)\\ 0 & (i \neq j)\\ \end{cases} \]
を満たしていることになります。
この式を見てみるとなんとなく行列の積をつくる計算と似ている感じがします。
添字の付き方によく注意して考えると、
\[ \left( \begin{array}{cccc} p_{ 11 } & p_{ 21 } & \ldots & p_{ n1 } \\ p_{ 12 } & p_{ 22 } & \ldots & p_{ n2 } \\ \vdots & \vdots & \ddots & \vdots \\ p_{ 1n } & p_{ 2n } & \ldots & p_{ nn } \end{array} \right) \left( \begin{array}{cccc} \overline{p_{ 11 }} & \overline{p_{ 12 }} & \ldots & \overline{p_{ 1n }} \\ \overline{p_{ 21 }} & \overline{p_{ 22 }} & \ldots & \overline{p_{ 2n }} \\ \vdots & \vdots & \ddots & \vdots \\ \overline{p_{ n1 }} & \overline{p_{ n2 }} & \ldots & \overline{p_{ nn }} \end{array} \right) = \left( \begin{array}{cccc} 1 & 0 & \ldots & 0 \\ 0 & 1 & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & 1 \end{array} \right) \]
と書いて良いことがわかります。つまり、\(\lt \boldsymbol{b}_1,\boldsymbol{b}_2,\ldots,\boldsymbol{b}_n \gt\) が正規直交基底になるのは
\[ {}^t \! P\overline{P}=E_n \]
を満たしているときであることがわかりました。
以上を次の命題にまとめておきます。
命題
計量線形空間の正規直交基底 \(\lt \boldsymbol{u}_1,\boldsymbol{u}_2,\ldots,\boldsymbol{u}_n \gt\) から基底変換の行列 \(P\) によって 基底 $_1,_2,,_n $ をつくるとき、\(\lt \boldsymbol{b}_1,\boldsymbol{b}_2,\ldots,\boldsymbol{b}_n \gt\) が正規直交基底になるのは基底の変換行列 \(P\) が
\[ {}^t \! P\overline{P}=E_n \]
を満たしているときです。
定義
正方行列 \(U\) が\[ {}^t \! \overline{U}U=U{}^t \! \overline{U}=E_n \]
を満たすとき \(U\) はユニタリー行列と呼ばれます。
補足
- 一般に正方行列 \(A,B\) に対して \(AB=E\) が成りたてば \(BA=E\) も成り立つことを以前証明しました。 ですから、 \({}^t \! \overline{U}U=E\) が成り立てば \(U{}^t \! \overline{U}=E\) も成り立ち、\(U{}^t \! \overline{U}=E\) が成り立てば \({}^t \! \overline{U}U=E\) も成り立ちます。
- 一般に行列 \(A,B\) に対して \(\overline{AB}=\bar{A}\bar{B}\) が成り立ちます。 ですから
\[ {}^t \! \overline{U}U=E \Leftrightarrow \overline{{}^t \! \overline{U}U}=\overline{E} \Leftrightarrow {}^t \! \overline{\overline{U}}\overline{U}=E \Leftrightarrow {}^t \! U\overline{U}=E \]
が成り立ちます。
- これらより、正規直交基底から正規直交基底への基底変換行列はユニタリー行列であるということができます。
まとめ
計量線形空間では内積を使って、任意の \(k\) 個の一次独立なベクトル \(\boldsymbol{a}_1,\boldsymbol{a}_2,\ldots,\boldsymbol{a}_k\) から、上で説明した手順に従い次のような条件を満たす \(V\) の \(k\) 個のベクトル \(\boldsymbol{u}_1,\boldsymbol{u}_2,\ldots,\boldsymbol{u}_k\) をつくることができます。
- \(\boldsymbol{u}_1,\boldsymbol{u}_2,\ldots,\boldsymbol{u}_k\) はどれも \(\boldsymbol{a}_1,\boldsymbol{a}_2,\ldots,\boldsymbol{a}_k\) の一次結合となっている。
- \(\boldsymbol{u}_1,\boldsymbol{u}_2,\ldots,\boldsymbol{u}_k\) は互いに直交する。
- \(\boldsymbol{u}_1,\boldsymbol{u}_2,\ldots,\boldsymbol{u}_k\) の長さはどれも \(1\) である。
これはグラム・シュミットの直交化と呼ばれています。
計量線形空間の基底が内積に関して、
- 異なるベクトルは互いに直交している
- 基底の各ベクトルの長さは \(1\)
という条件を満たしているとき、その基底は正規直交基底と呼ばれます。
\(\mathbb{K}\) 上の有限次元計量線形空間には正規直交基底が存在します。
計量線形空間の内積に関する正規直交基底を用いてベクトルを座標で扱うと、その内積の座標による表示は数ベクトル空間の自然内積と同じ見かけになります。
計量線形空間のある正規直交基底からある基底変換の行列 \(P\) を使って別の基底をつくるとき、つくられた基底が正規直交基底になるのは基底の変換行列 \(P\) が\[ {}^t \! P\overline{P}=E_n \]
を満たしているときです。
正方行列 \(U\) が\[ {}^t \! \overline{U}U=U{}^t \! \overline{U}=E_n \]
を満たすとき \(U\) はユニタリー行列と呼ばれます。
正規直交基底から正規直交基底への基底変換行列はユニタリー行列です。
計量の入った線形空間