空間のベクトルの空間の一次写像と行列

2022-05-04

ここでは空間のベクトルの空間 \(V^3\) の一次写像について考えます。前回に説明した平面のベクトルの空間 \(V^2\) の場合と同様な話が成り立つことがわかります。

\(V^3\)の一次写像

空間のベクトルの空間 \(V^3\) のどのベクトルに対してもある新しいベクトルを対応させる決まり \(f\) のうち

\[ \begin{eqnarray} f(\boldsymbol{u}+\boldsymbol{v}) &=& f(\boldsymbol{u})+f(\boldsymbol{v})\\ f(r\boldsymbol{u}) &=& rf(\boldsymbol{u}) \end{eqnarray} \] という性質をもつものを \(V^3\) の一次写像といいます。

例

空間の中のどこかに原点 \(\mathrm{O}\) を定めておきます。図を描いたりして想像すればわかりますが、次の「決まり」はどれも \(V^3\) の一次写像です。

• \(V^3\) のベクトル \(\boldsymbol{u}\) に対して \(\mathrm{O}\) に関して（点）対象なベクトルを対応させる。（原点に関する対称移動）
• \(\mathrm{O}\) を通るある平面 \(H\) を考え、\(V^3\) のベクトル \(\boldsymbol{u}\) に対して \(H\) に関し（面）対象なベクトルを対応させる。（ある平面に関する鏡映）
• \(\mathrm{O}\) を通るある向きのついた直線 \(\ell\) を考え、\(V^3\) のベクトル \(\boldsymbol{u}\) に対して 、\(\mathrm{O}\) から \(\ell\) の進む方向を見て\(\ell\) を軸として反時計回りに\(\alpha\) 回転させたベクトルを対応させる。（ある直線に関する回転移動）

例えば、原点に関する対称移動は、

• 2つのベクトルを足してから原点に関して対称移動したものと、2つのベクトルをそれぞれ原点に関して対称移動してから足したものは一致する
• あるベクトルを何とか倍してから原点に関する対称移動をしたものと、あるベクトルを原点に関して対称移動してからナントカ倍したものは一致する

という性質をもっていることは、図を想像したりすれば悟ることができるでしょう。

座標系を設けて \(V^3\) の一次写像を行列で表現する

\(V^3\) の幾何ベクトルを数ベクトルで扱う

空間に、必ずしも直交していない座標系を設けることにしましょう。

\(y\) 軸と \(z\) 軸を含む平面を \(yz\) 面、\(z\) 軸と \(x\) 軸を含む平面を \(zx\) 面、\(x\) 軸と \(y\) 軸を含む平面を \(xy\) 面と呼ぶことにします。

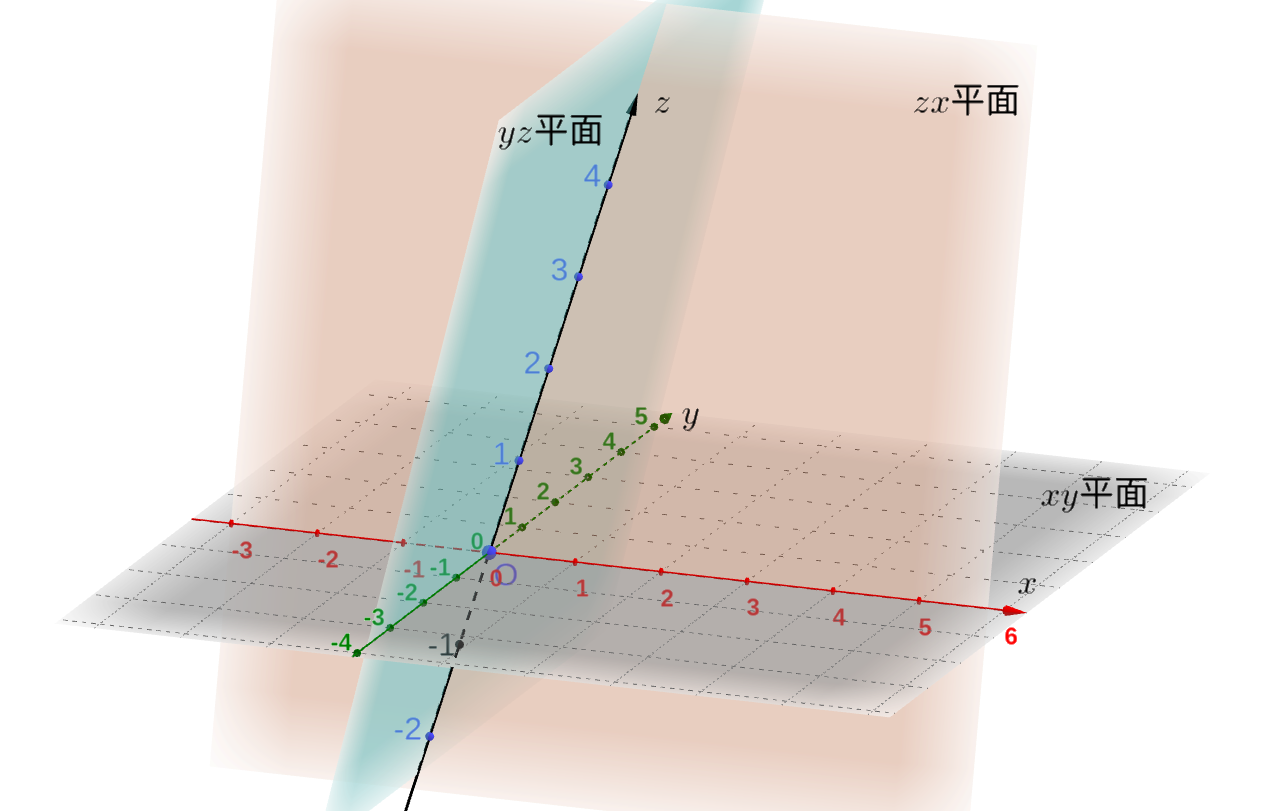
たとえ軸どうしが直交していないとしても、この座標系を使うと以下説明するようにして \(V^3\) の幾何ベクトルに数ベクトルを対応させることができます。

\(\boldsymbol{u}\) を \(V^3\) の幾何ベクトルとし、原点を始点とする矢印で代表させます。

この矢印の終点を通り \(yz\) 面に平行な平面を考えます。この平面と \(x\) 軸はある場所で交わりますが 交点で \(x\) 軸の目盛りを読み取ります。

同様にして、終点を通り\(zx\) 面に平行な平面と \(y\) 軸との交点の目盛り、終点を通り\(xy\) 面に平行な平面と \(z\) 軸との交点の目盛りを読み取ります。

以上のようにすると3つの数が得られますがここではそれらを \(x,y,z\) であらわすことにします。

そしてこれら3つの数を縦に並べ、カッコでくくることにより \(\boldsymbol{u}\) に対応する数ベクトル \(\left( \begin{array}{r} x\\ y\\ z \end{array} \right)\) が得られます。

（座標系を違うものに取り替えると、得られる数ベクトルも異なるものになることは容易に想像できるでしょう。）

\(V^3\) の対称移動を行列で表現する

ではここで、\(V^3\) の一次写像の例として原点 \(\mathrm{O}\) に関する対称移動を考えることにします。そしてこの一次写像を \(f\) であらわすことにします。

空間の中に必ずしも直交していない座標系を設けておきます。そして\(\boldsymbol{u}\) をあらわす数ベクトルと \(f(\boldsymbol{u})\) ををあらわす数ベクトルをそれぞれ、

\[\boldsymbol{u}=\left( \begin{array}{r} x\\ y\\ z \end{array} \right) ,\quad f(\boldsymbol{u})=\left( \begin{array}{r} x'\\ y'\\ z' \end{array} \right) \]

とおくことにします。

座標系の描かれている図を自分で描いてみるととわかりますが、\(f(\boldsymbol{u})\) は \(\boldsymbol{u}\) を \(\mathrm{O}\) に関して対称移動したものなので、それぞれの数ベクトルの間には

\[\left( \begin{array}{r} x'\\ y'\\ z' \end{array} \right) = \left( \begin{array}{r} -x\\ -y\\ -z \end{array} \right) \]

の関係があります。（これは、原点に関する対称移動はどの幾何ベクトルも長さを変えずに逆向きに移動することを考えてみればほとんど明らかでしょう。）

この関係は行列をもちいてあらわすと、

\[\left( \begin{array}{r} x'\\ y'\\ z' \end{array} \right) = \begin{pmatrix} -1 & 0 & 0 \\ 0 & -1 & 0\\ 0 & 0 & -1 \end{pmatrix} \left( \begin{array}{r} x\\ y\\ z \end{array} \right) \]

であることがわかります。

\(V^3\) の回転を行列で表現する

では別の一次写像の例として、空間に右手系の正規直交座標系を設定して、 \(z\) 軸に関する角 \(\alpha\) の回転のことを考えてみることにしましょう。

この回転をあらわす一次写像を \(f\) とし、幾何ベクトル \(\boldsymbol{u}\) に対応する数ベクトルと 幾何ベクトル \(f(\boldsymbol{u})\) に対応する数ベクトルをそれぞれ、

\[\boldsymbol{u}=\left( \begin{array}{r} x\\ y\\ z \end{array} \right) ,\quad f(\boldsymbol{u})=\left( \begin{array}{r} x'\\ y'\\ z' \end{array} \right) \] とおくことにします。

右手系の正規直交座標系が描かれている図を自分で描いてみるとわかりますが、\(\boldsymbol{u}\) の終点が \(z\) 軸に関して角 \(\alpha\) だけ回転して \(f(\boldsymbol{u})\) の終点ができるわけですから \(z\) の値は変わりません。ですから、\(x\) と \(y\) がどうなるかということを \(xy\) 平面の回転を思い出して考えれば十分です。そうすると、それぞれの数ベクトルの間には

\[\left( \begin{array}{r} x'\\ y'\\ z' \end{array} \right) = \left( \begin{array}{c} \cos\alpha\cdot x - \sin\alpha\cdot y\\ \sin\alpha\cdot x + \cos\alpha\cdot y\\ z \end{array} \right) \] の関係がありことがわかります。

この関係は行列をもちいてあらわすと、 \[\left( \begin{array}{r} x'\\ y'\\ z' \end{array} \right) = \begin{pmatrix} \cos\alpha & -\sin\alpha & 0 \\ \sin\alpha & \cos\alpha & 0\\ 0 & 0 & 1 \end{pmatrix} \left( \begin{array}{r} x\\ y\\ z \end{array} \right) \]

であることがわかります。

基底を用いて \(V^3\) の一次写像を行列で表現する

$ V^3$ の一次写像 \(f\) があるとします。

\(V^3\) の基底 \(<\boldsymbol{a}, \boldsymbol{b},\boldsymbol{c}>\) を用意します。（零ベクトルではない 3つのベクトル \(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}\) でどのように平行移動してもある1つの平面には乗せられないものを用意すれば良いわけですね。）

\(V^3\) のどんなベクトル \(\boldsymbol{u}\) も適切な 3つの数 \(x,y,z\) を用いて、 \[\boldsymbol{u} = x\,\boldsymbol{a} + y\,\boldsymbol {b} + z\,\boldsymbol{c}\] のように一意に書くことができます。そして、この基底 \(<\boldsymbol{a}, \boldsymbol{b},\boldsymbol{c}>\) を使ったときの \(\boldsymbol{u}\) に対応する数ベクトルは

\[ \boldsymbol{u} =\left( \begin{array}{r} x\\ y\\ z \end{array} \right) \]

となっています。

また、\(f(\boldsymbol{u})\) も \(V^3\) のベクトルですから 適切な 3つの数 \(x',y',z'\) を用いて、\[f(\boldsymbol{u} )= x'\boldsymbol{a} + y'\boldsymbol{b} + z'\boldsymbol{c}\] と一意に書けるはずです。そうすると、基底 \(<\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}>\) を使ったときの \(f(\boldsymbol{u})\) に対応する数ベクトルは \[ f(\boldsymbol{u}) =\left( \begin{array}{r} x'\\ y'\\ z' \end{array} \right) \] とあらわされます。

\(f\) は \(V^3\) の一次写像ですから、 \[ \begin{eqnarray} f(\boldsymbol{u}) &=& f( x \boldsymbol{a} + y \boldsymbol{b}+z\boldsymbol{c})\\ &=& f( x \boldsymbol{a} )+f( y \boldsymbol{b})+f(z\boldsymbol{c})\\ &=&xf(\boldsymbol{a}) + yf( \boldsymbol{b})+zf( \boldsymbol{c}) \end{eqnarray} \]

という計算が成り立ちます。 この式は、どんなベクトル \(\boldsymbol{u}\) の \(f\) による行き先 \(f(\boldsymbol{u})\)も、基底として選んだ 3つのベクトル \(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}\) の行き先 \(f(\boldsymbol{a}),f(\boldsymbol{b}),f(\boldsymbol{c})\) によって決定されるということを主張しています。

そしてこの式にあらわれる \(f(\boldsymbol{a}),f(\boldsymbol{b}),f(\boldsymbol{c})\) は \(V^3\) のベクトルですから、全部で 9つの適当な数 \(k,l,m,p,q,r,u,v,w\) を用いて、

\[ \begin{eqnarray} f(\boldsymbol{a})&=&k\boldsymbol{a}+ l\boldsymbol{b}+m\boldsymbol{c}\\ f(\boldsymbol{b})&=&p\boldsymbol{a}+q\boldsymbol{b}+r\boldsymbol{c}\\ f(\boldsymbol{c})&=&u\boldsymbol{a}+v\boldsymbol{b}+w\boldsymbol{c} \end{eqnarray} \]

とあらわされるはずです。

ですから、

\[ \begin{eqnarray} f(\boldsymbol{u}) &=&xf(\boldsymbol{a}) + yf( \boldsymbol{b}) + zf(\boldsymbol{c})\\ &=&x(k\boldsymbol{a}+ l\boldsymbol{b}+m\boldsymbol{c}) + y(p\boldsymbol{a}++q\boldsymbol{b}+r\boldsymbol{c})+z(u\boldsymbol{a}+v\boldsymbol{b}+w\boldsymbol{c})\\ &=&(xk+yp+zu)\boldsymbol{a} + (xl+yq+zv)\boldsymbol{b}+(xm+yr+zw)\boldsymbol{c} \end{eqnarray} \]

と計算できます。 そして、 基底 \(<\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}>\) を使ったときの \(f(\boldsymbol{u})\) に対応する数ベクトルは

\[ f(\boldsymbol{u}) =\left( \begin{array}{c} xk+yp+zu\\ xl+yq+zv\\ xm+yr+zw \end{array} \right) \]

となります。 以上より、

\[ \left( \begin{array}{r} x'\\ y'\\ z' \end{array} \right) = \left( \begin{array}{c} xk+yp+zu\\ xl+yq+zv\\ xm+yr+zw \end{array} \right) \]

であることがわかりますが、行列の計算を知っていれば、これは

\[ \left(\begin{array}{r} x'\\ y'\\ z' \end{array} \right) = \begin{pmatrix} k & p & u\\ l & q & v \\ m & r & w \end{pmatrix} \left(\begin{array}{r} x\\ y\\ z \end{array} \right) \]

と書いてあるのと同じであることがわかるでしょう。

ここに現れた行列 \(\begin{pmatrix} k & p & u\\ l & q & v \\ m & r & w \end{pmatrix}\) を一次最後 \(f\) をあらわす行列といいます。

ここで注目したいのは、一次写像 \(f\) あらわす行列の第一列には \(f(\boldsymbol{a})\) に対応する数ベクトル、第二列には \(f(\boldsymbol{b})\) に対応する数ベクトル、第三列には \(f(\boldsymbol{c})\) に対応する数ベクトルが現れているということです。

\(z\) 軸のまわりの回転をあらわす行列

ではここで、回転を取り扱うのに都合の良い基底 \(<\boldsymbol{e}_1, \boldsymbol{e}_2, \boldsymbol{e}_3>\) を使うことにします。（これらはそれぞれ、直交する \(x,y,z\) 軸にそって正の向きに長さ \(1\) だけ進む矢印であらわされるベクトルです。） そして、これを使って、\(z\) 軸に関する角 \(\alpha\) の回転 \(f\) を行列であらわすとどうなるのか考えてみたいと思います。

\(z\) 軸方向のベクトル \(\boldsymbol{e_3}\) は動かないままで、\(\boldsymbol{e_1}\) と \(\boldsymbol{e_2}\) は \(xy\) 平面内で原点の周りに各 \(\alpha\) 回転するだけなので図を描いてみると、

\[ \begin{eqnarray} f(\boldsymbol{e}_1)&=&\cos\alpha\cdot\boldsymbol{e}_1+ \sin\alpha\cdot\boldsymbol{e}_2 +0\cdot\boldsymbol{e}_3\\ f(\boldsymbol{e}_2)&=&-\sin\alpha\cdot\boldsymbol{e}_1 +\cos\alpha\cdot\boldsymbol{e}_2+0\cdot\boldsymbol{e}_3\\ f(\boldsymbol{e}_3)&=&0\cdot\boldsymbol{e}_1+0\cdot\boldsymbol{e}_2+1\cdot\boldsymbol{e}_3 \end{eqnarray} \]

となることがわかります。 これから \(f\) をあらわす式は \[\left( \begin{array}{r} x'\\ y'\\ z' \end{array} \right) = \begin{pmatrix} \cos\alpha & -\sin\alpha & 0 \\ \sin\alpha & \cos\alpha & 0\\ 0 & 0 & 1 \end{pmatrix} \left( \begin{array}{r} x\\ y\\ z \end{array} \right) \]

となることがわかります。

まとめ

空間のベクトルの空間 \(V^3\) のどのベクトルに対してもある新しいベクトルを対応させる決まり \(f\) のうち

\[ \begin{eqnarray} f(\boldsymbol{u}+\boldsymbol{v}) &=& f(\boldsymbol{u})+f(\boldsymbol{v})\\ f(r\boldsymbol{u}) &=& rf(\boldsymbol{u}) \end{eqnarray} \]

という性質をもつものを \(V^3\) の一次写像といいます。

空間に何らかの座標系を設けることにより、幾何ベクトルは数ベクトルで、一次写像は行列であらわすことができます。

\(V^3\) に何らかの 基底\(<\boldsymbol{a}, \boldsymbol{b},\boldsymbol{c}>\) を決めておくと、一次写像 \(f\) の 挙動は \(f(\boldsymbol{a}),f(\boldsymbol{b}),f(\boldsymbol{c})\) がどんなベクトルになるのかを調べればすべてわかってしまいます。

\(V^3\) の何らかの基底を（座標系の代わりに）決めることにより、幾何ベクトルは数ベクトルで、一次写像は行列であらわすことができます。

幾何ベクトルを（縦に数が並んだ）数ベクトルであらわし、一次変換を行列であらわす場合、ベクトルに行列を左から掛けることにより変換後の数ベクトルが得られます。

右手系の直交座標系や基底 \(<\boldsymbol{e}_1, \boldsymbol{e}_2,\boldsymbol{e}_3>\) を使うと 回転を考えるときに便利です。